I’ve curated a stunning collection of 100 Google Earth images from the illustrious book Overview for your viewing pleasure! …
These books demystify complex concepts, illustrate the application of math in various fields, and share stories of mathematical discovery that inspire awe and wonder….
The 20+ history of science books listed below promise more than just an academic foray into the chronicles of scientific inquiry; they serve as a testament to the nobility of…
In this compilation, I present the top 10 Islamic geometry books, each offering a unique perspective on this captivating subject….
The books about bees listed here are but a few samples of the delightful troves of bee literature that await the curious reader. As you turn the pages of these…
This list of books about application of mathematics illuminates the diverse applications of mathematics, showcasing how this abstract science shapes our reality, influences various fields of research, and addresses complex…
In this guide, I delve into the best 5 graphing calculators that stand out in their field, helping engineers and students alike to achieve their academic and professional goals effectively….
Below I’ve curated a list of the seven best artificial intelligence books, perfect for those keen to learn about the intriguing world of AI, its capabilities, mysteries, and its potential…
A love for science often begins with a captivating book and the ones listed here have the power to ignite that spark. These science books are not only the highest-rated…
Help us exist with
Patreon
Get Abakcus straight to your inbox
Featured Directories

Seven of Albert Einstein’s Favorite Books
What are the books which affected Einsteins' thinking more? I did some search for you and listed Einstein's seven favorite books for you!

7 Utterly Well-written Math Books About Pi
Math books made me a huge believer in mathematics! Math shouldn't be only accessible for only math students because mathematics has a huge potential to be wildly interesting to anyone.…
Best Products
When it comes to buying any kind of tech, it’s easy to pick the wrong thing. That’s where our experts and testing team come in to help guide your buying decisions.
Watch

Toposcape
An audiovisual piece made up of over four thousand still images pulled from Google Earth, individually edited, and then manually sequenced to Midnight by Caravan Palace.

Braving the Chill: -37F Winter in Yellowstone National Park
Winter in Yellowstone transforms into a land of extremes: the collision of boiling water from the park’s famed geysers with the Frost King’s touch creates an ethereal tableau of steam…
- Nature ,

The Physics of Kung Fu
In an intersection of martial arts and digital artistry, Tobias Gremmler, a German visual artist, captures the spirit of Kung Fu through his captivating digital renderings.
Tools
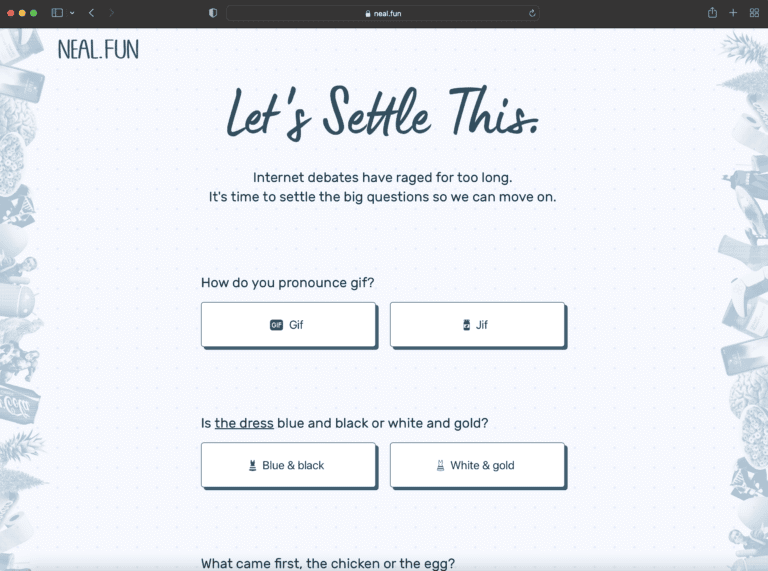
Let’s Settle This
Neal Agarwal is the brain behind the innovative website, Let's Settle This. This website offers internet users a chance to settle debates and help us move on from arguments that…

Kahoot
Kahoot! is a game-based learning platform that brings engagement and fun to 1+ billion players every year at school, at work, and at home.
Featured Books
Listen
Make Math Moments Matter
Kyle Pearce and Jon Orr uncover how we can Make Math Moments That Matter for every student in the math classroom from K-12.
- Education ,
- Mathematics ,

Ask us Anything
The Ask Us Anything podcast by Popular Science is the perfect opportunity for listeners to satiate their curiosity about the world around them. Each episode features experts in a particular…
DIY

How to Make a Rocket Man?
Kids love space, and most of them want to be an astronaut! You can build a space rocket by using items already around the house. Talented blogger and mum Kate…

How to Make Color-Coded After School Routine Clock
We have been checking out these color-coded after school routine clocks on Pinterest for quite a while. Similar to an alarm clock, these clocks are designed to keep the kids’…

How to Measure The Speed Of Light?
Measure the speed of light using chocolate and a microwave oven. Microwaves work by creating standing waves inside the microwave oven. The water molecules in the chocolate try to align…




















