Depending on your philosophical views on time and calendars and so on, today is something like the 4.5 billionth Pi Day that Earth has witnessed. But that long history is nothing compared to the infinity of pi itself.
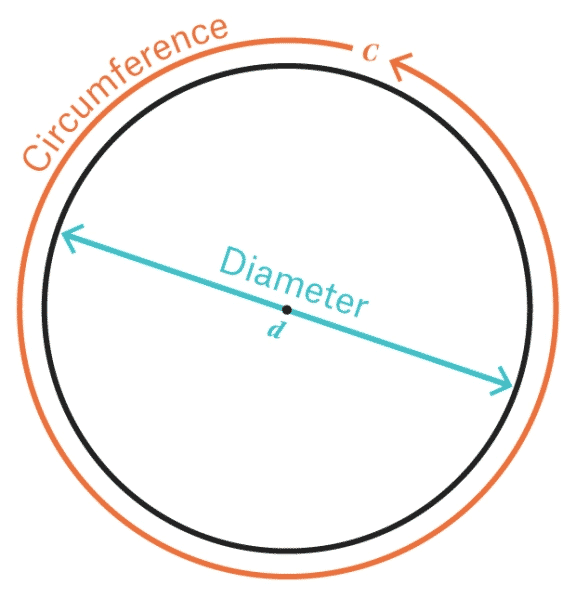
A refresher for those of you who have forgotten your seventh-grade math lessons1: Pi, or the Greek letter ?, is a mathematical constant equal to the ratio of a circle’s circumference to its diameter — C/d. It lurks in every circle, and equals approximately 3.14. (Hence Pi Day, which takes place on March 14, aka 3/14.)
But the simplicity of its definition belies pi’s status as the most fascinating, and most studied, number in the history of the world. While treating pi as equal to 3.14 is often good enough, the number really continues on forever, a seemingly random series of digits ambling infinitely outward and obeying no discernible pattern — 3.14159265358979…. That’s because it’s an irrational number, meaning that it cannot be represented by a fraction of two whole numbers (although approximations such as 22/7 can come close).
But that hasn’t stopped humanity from furiously chipping away at pi’s unending mountain of digits. We’ve been at it for millennia.
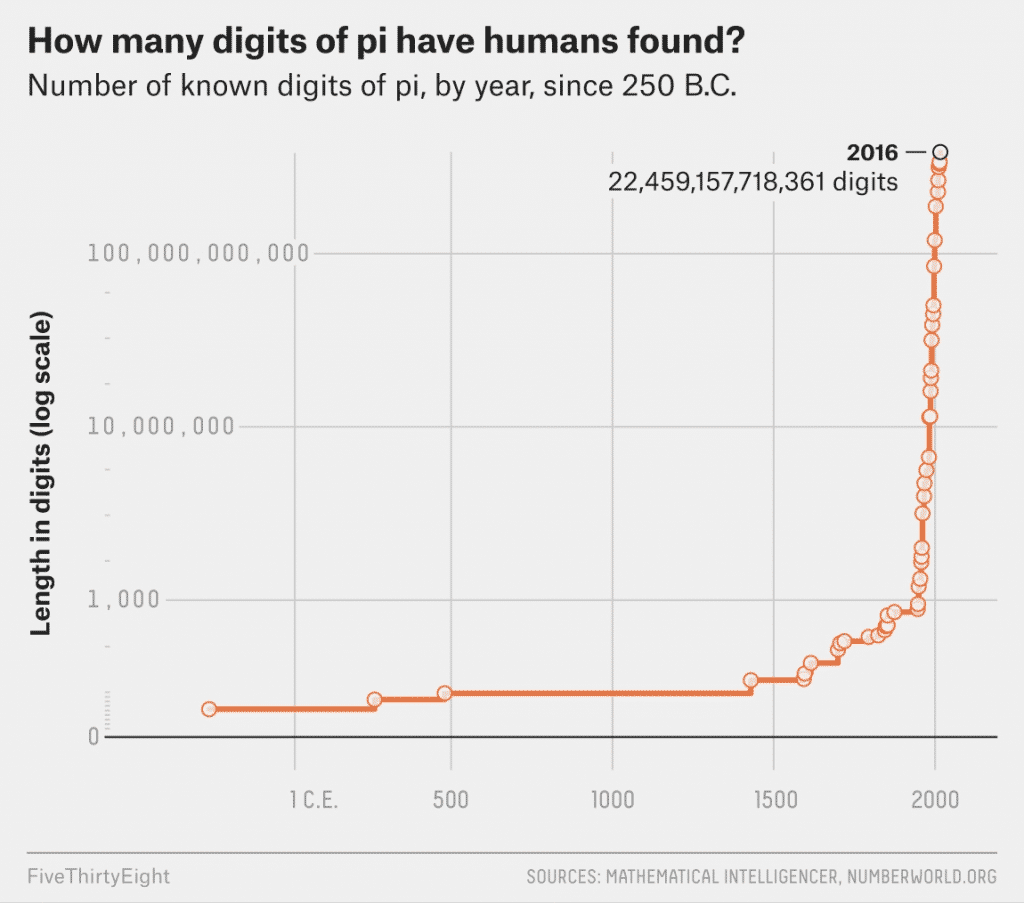
People have been interested in the number for basically as long we’ve understood math. The ancient Egyptians, according to a document that also happens to be the world’s oldest collection of math puzzles, knew that pi was something like 3.1. A millennium or so later, an estimate of pi showed up in the bible: The Old Testament, in 1 Kings, seems to imply that pi equals 3: “And he made a molten sea, ten cubits from the one brim to the other: it was round all about … and a line of thirty cubits did compass it round about.”
Archimedes, the greatest mathematician of antiquity, got as far as 3.141 by around 250 B.C. Archimedes approached his calculation of pi geometrically, by sandwiching a circle between two straight-edged regular polygons. Measuring polygons was easier than measuring circles, and Archimedes measured pi-like ratios as the number of the polygons’ sides increased, until they closely resembled circles.