Archimedes used calculus as a simple way of thinking that was never seen before. On the other hand, Richard Feynman held that calculus was the language that God had used when creating this universe. In reality, both are correct. Not only is calculus a form of thinking, but it is also a way to explain an unknown occurrence. If we look further into it, we can assume that they are the same thing. After all, language is the spoken form of thoughts. (Let us ignore those who talk without thinking).
Ever since Leibniz proposed calculus to the world, mathematicians and physicists alike have applied calculus to physics laws that they believed to be true, that they could not prove, however. Aside from that, those with a grasp of mathematical thinking have always used calculus’s foundation, mathematical thinking, to solve complex problems around them.
Therefore it is no exaggeration to say that anything and everything around us is tied to calculus.
Calculus deals with things that are constantly changing. More specifically, calculus analyzes constant changes and helps us act with more foresight. It also helps us find optimal solutions to problems that occur because of continuous changes.
The calculus we use and teach today is split into two main branches: differential calculus and integral calculus. These two are like opposite siblings to each other. That is because if you take the derivative of a function and then take the integral of it, you return to where you started.
Differential calculus deals with the concept of rate of change. Meaning it aids us in finding an instantaneous change in a given timeframe. Examples of this include continually changing things that we need to make graphs of. Blood pressure, heart rate, stock markets, the weight of rockets, the speed of a runner, air pressure and temperature, the population of bacteria are some of the many vital examples. We use differential calculus when analyzing the curved graphs, or parabolas, that map these events to find instantaneous rate. That means that if we zoom in far enough into a parabola and see a linear line, we can find the average or the slope. An example of this is if you look at a photograph of Usain Bolt running, you don’t see him running. However, it is clear that he is running. To find the speed at which he is running at that exact instance (instantaneous rate), we use differential calculus.
In integral calculus, however, we find the curved area between two determined points. Any elementary student can find the area of a square. Yet, to find the area of a curved section, we have to split the graph into as many, even infinitely many, rectangles. After that, we find and add the areas of said rectangles together to find a very accurate estimate for the section’s area.
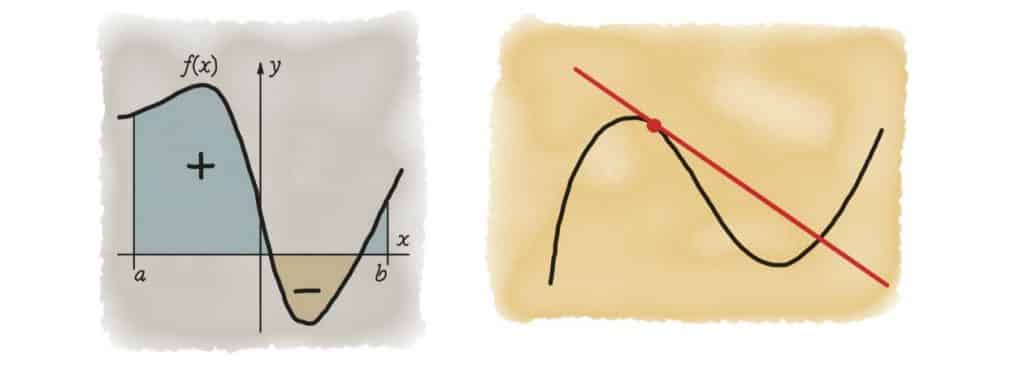
In this article, I will talk about calculus’s applications, a subject that I have been researching for a long time and have tried to simplify above. I want to mention that I have greatly benefited from the lectures of incredible mathematicians such as Ali Nesin and Steven Strogatz while writing this article. I will attempt to share with you, in my own words, the examples that they taught their students during their lessons.