A circle is a closed two-dimensional figure with a center where all the points in the plane are equidistant. Some examples of circles are wheels, pizzas, circular ground, etc. The area of a circle formula is useful for measuring the space occupied by a circular field or a plot.
Suppose you have the plot to fence it, then the area formula will help you to check how much fencing is required. Or suppose you have to buy a table cloth, then how many portions of cloth are needed to cover it completely.
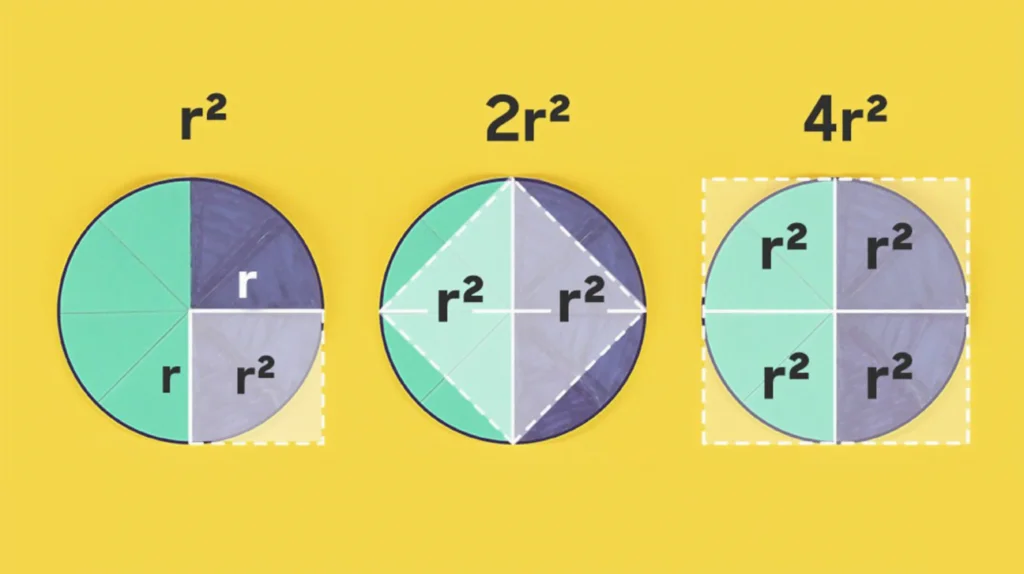
But why is the area of a circle pi times the square of the radius? The usual definition of pi is the ratio of the circumference of a circle to its diameter so that the circumference of a circle is pi times the diameter, or two pi times the radius.
This amazing DIY project shows that a circle can be cut and rearranged to closely resemble a parallelogram with height r and base pi times r by dividing the circle into slices. If you do more slices, the approximation obtained in this manner would be even better. By the way, there is also another beautiful way to understand the math behind the area of a circle! You can check it out here.
I got this idea first from Steven Strogatz’s beautiful book, Infinite Powers, about the history of calculus when I was at college.
Ingredients:
Step 1

Step 2

Step 3

Step 4

Step 5

Step 6

Step 7
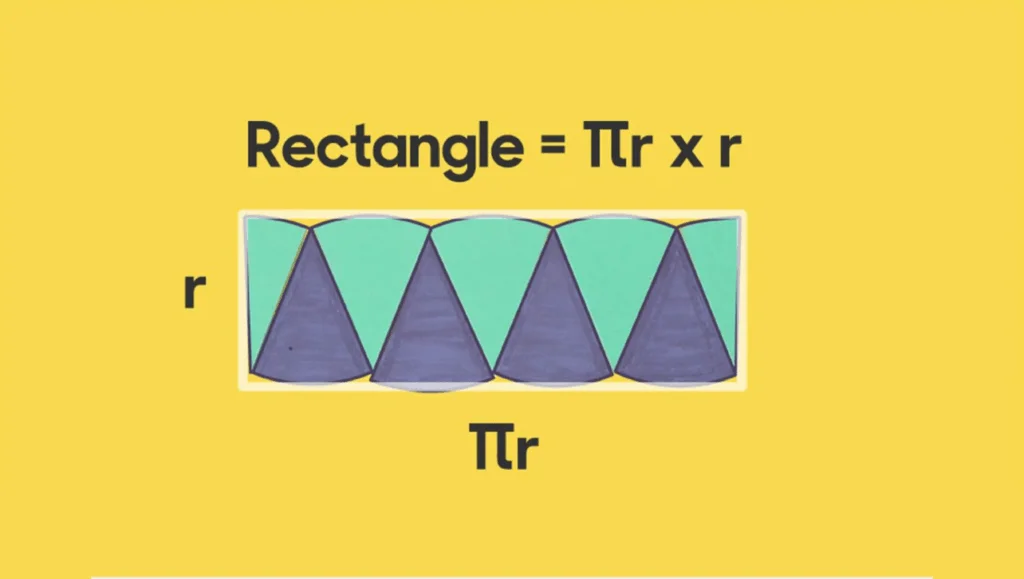
Step 8
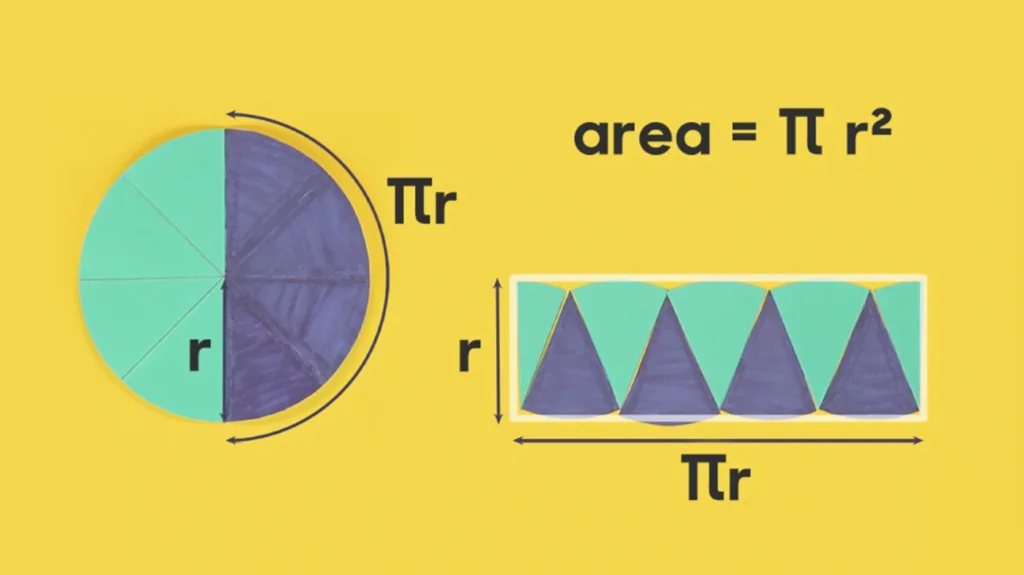
Step 9