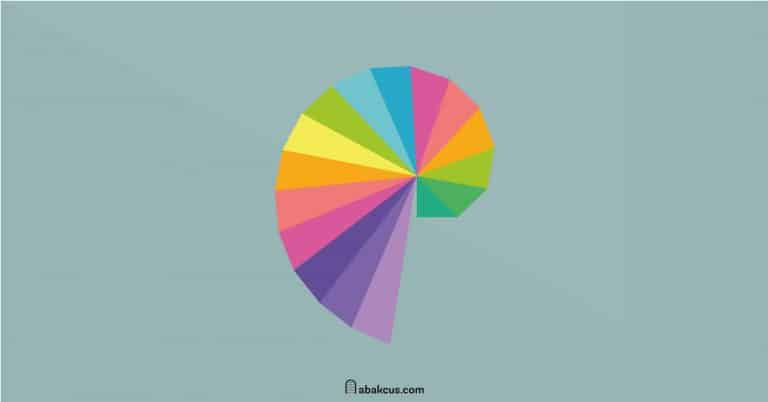The spiral of Theodorus is a spiral composed of right triangles. Hundreds of years ago, Theodorus of Cyrene constructed continuous right triangles and got a beautiful spiral. He used that spiral to prove that all non-square integers from 3-17 are irrational.

Constructing the spiral of Theodorus might be a good classroom activity. We have prepared the instructions for you.
Ingredients:
STEP 1
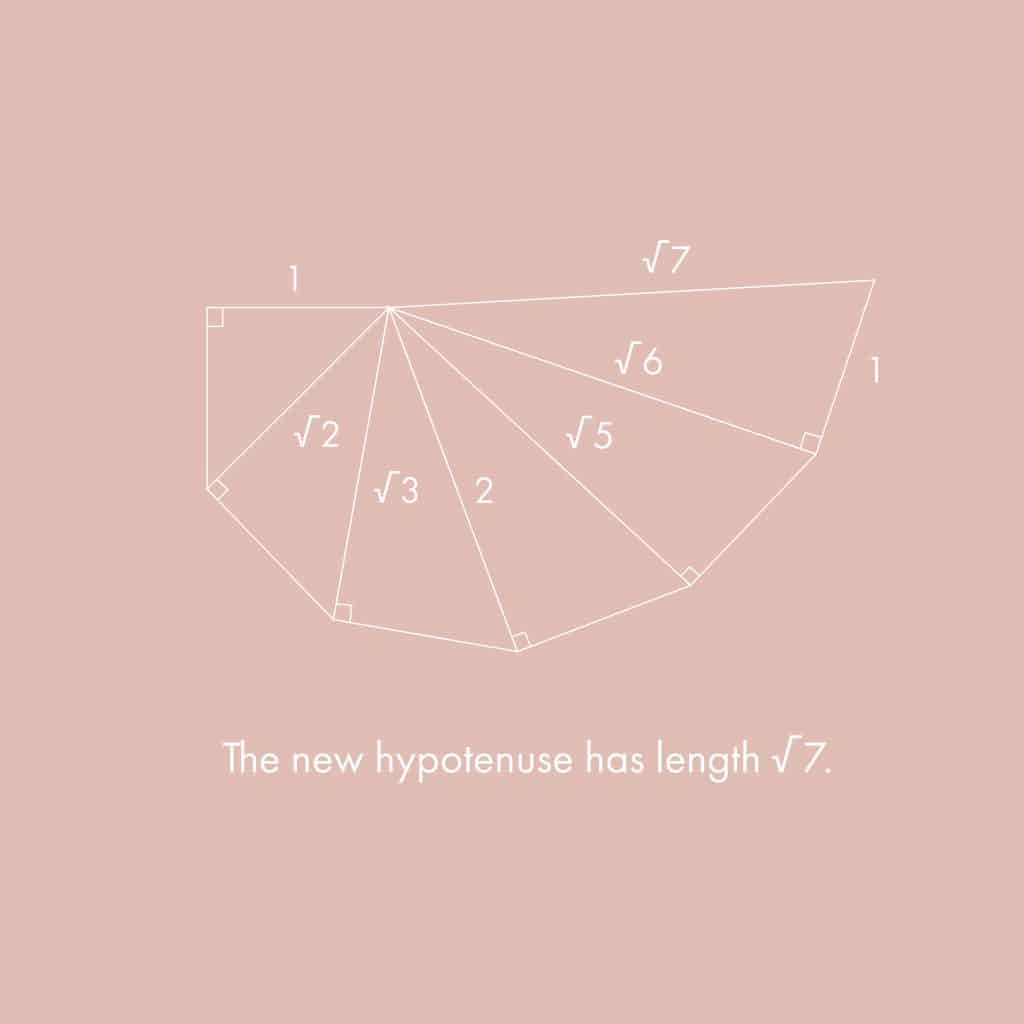
First, draw an isosceles right triangle with each leg having a unit length.

STEP 2
Then use the hypotenuse as the base of the second right triangle with the other leg having a length of 1.

STEP 3
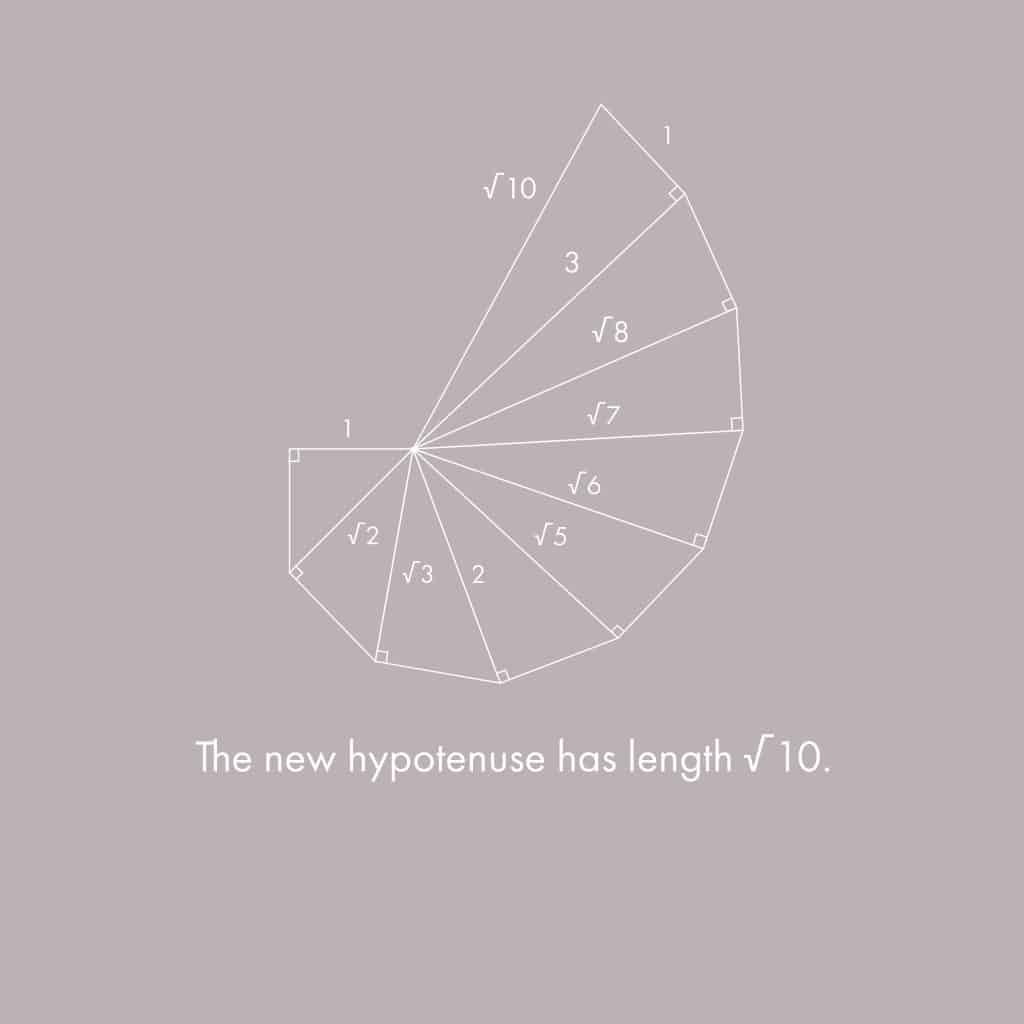
Repeat the process fifteen more times and get a beautiful spiral.

The original spiral stops at √17 because that is the last hypotenuse before overlapping. Erich Teuffel proved that no two hypotenuses will ever overlap regardless of how far the spiral continues.
Division of a Circle Into Five Equal Parts from Elizabeth Nelli
The spiral can also be used to solve the problem of splitting a circle into five equal parts. We begin by creating the radius of the first circle, which is √1. Just by creating the rest of the spiral, we can make the larger circles’ other radii.
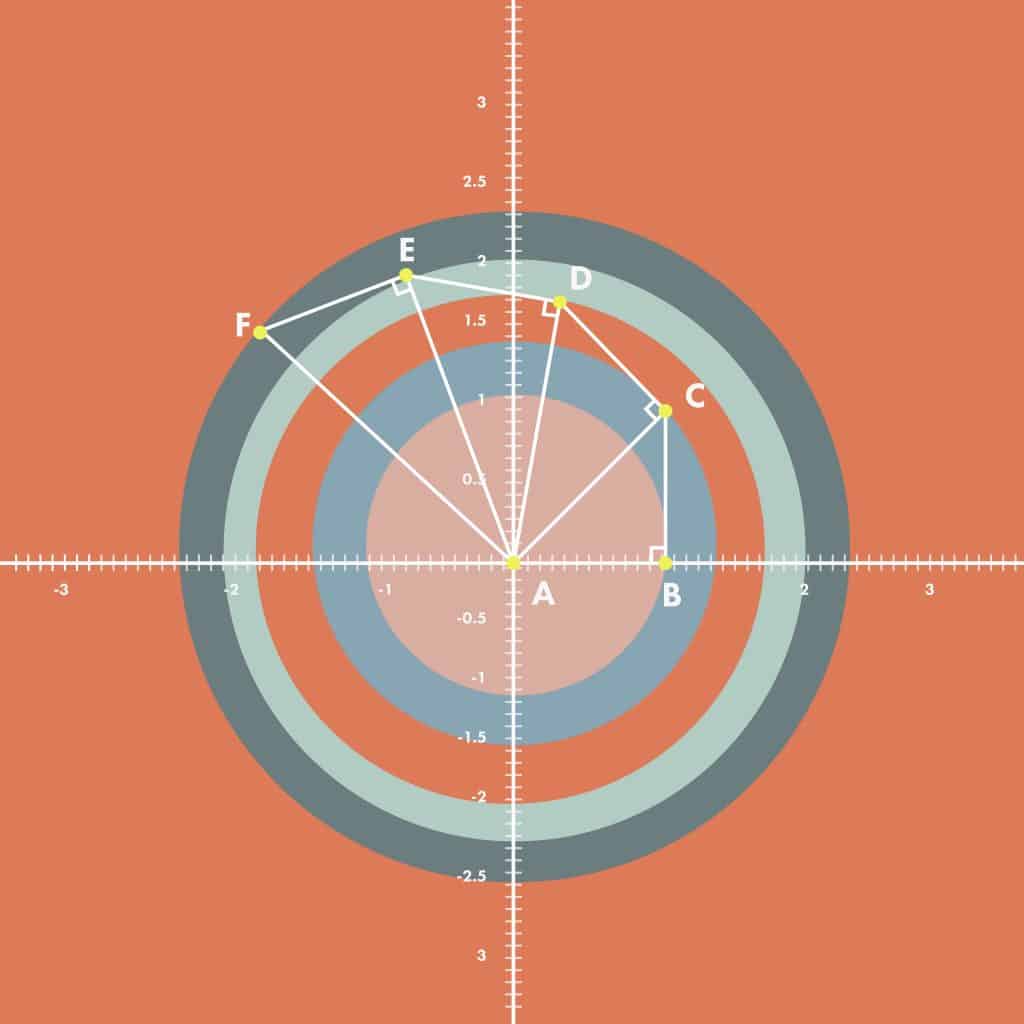
We can see using GSP calculations that all the areas of the five circles are equal. We start with the area of the innermost circle AB. Next, we calculate the area of circle AC. From there, we subtract the area of AB from the area of AC to see that the two are equal. This process can be done for each consecutive circle by removing the circle area lying directly on top of it.