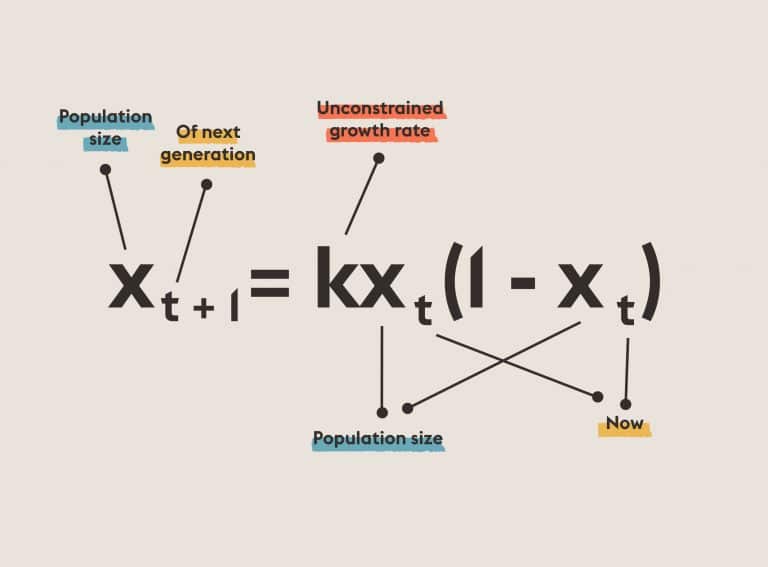
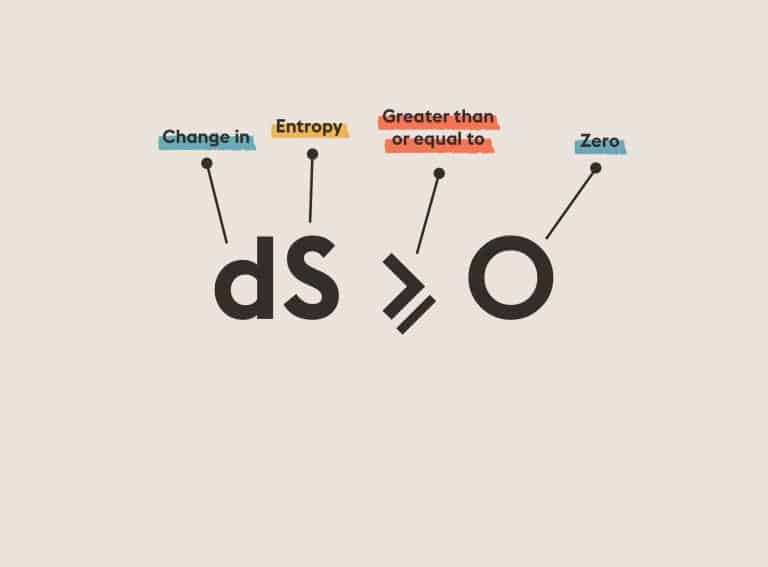
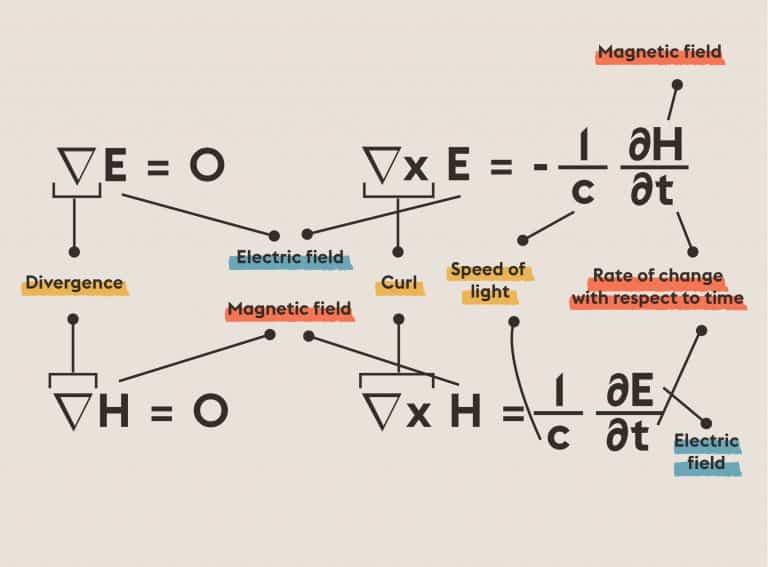
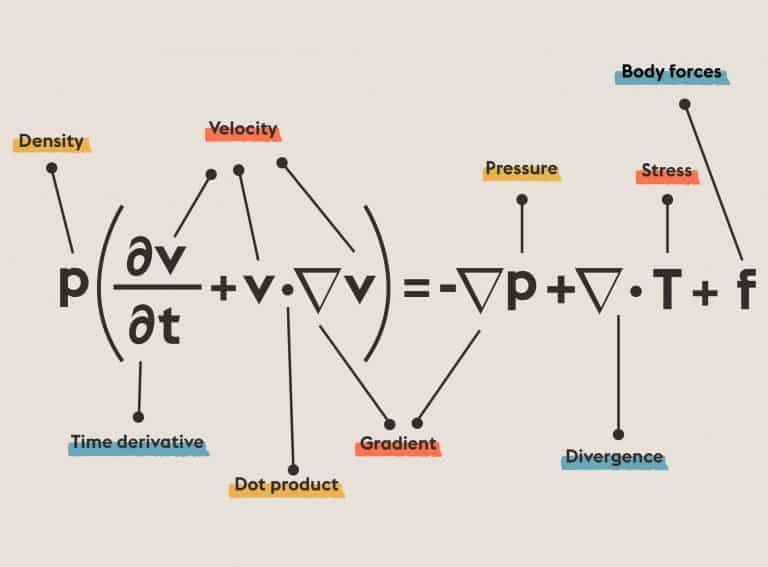
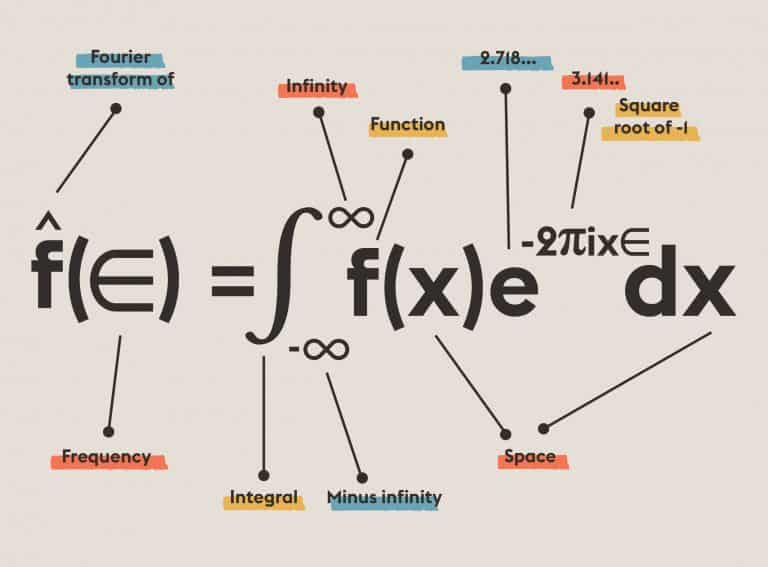
Information Theory

Information theory defines how much information a message contains regarding the probabilities with which the symbols that make it up are likely to occur. It ushered in the age of information. It established limits on the efficiency of communications, allowing engineers to stop looking for codes that were too effective to exist. It is basic to today’s digital communications—phones, CDs, DVDs, the Internet. Information theory led us to an efficient error-detecting and error-correcting codes, used in everything from CDs to space probes. Applications include statistics, artificial intelligence, cryptography, and extracting meaning from DNA sequences.

Similar Stuff

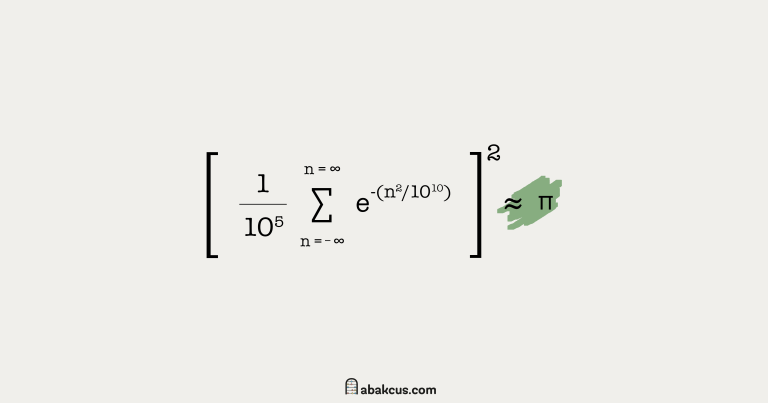
The Formula to Get 42 Billion Digits of π

The Formula to Get 42 Billion Digits of π

While writing "7 Utterly Well-written Math Books About Pi," I found a very interesting math formula that will give you 42 consecutive digits of π accurately but is still wrong.

Black-Scholes Equation | Equations That Changed the World

Black-Scholes Equation

Black-Scholes equation says how the price of financial derivative changes over time, based on the principle that when the price is correct.

Chaos Theory | Equations That Changed the World | Abakcus

Chaos Theory

Chaos theory models how a population of living creatures changes from one generation to the next, when there are limits to the available resources. It is one of the simplest…

Schrödinger's Equation | Equations That Changed the World

Schrödinger’s Equation

Schrödinger's equation says that the equation models matter not as a particle but as a wave and describes how such a wave propagates.

Relativity | Equations That Changed the World | Abakcus

Relativity

Einstein's relativity formula says that matter contains energy equal to its mass multiplied by the square of the speed of light.

Second Law of Thermodynamics | Equation That Changed the World

Second Law of Thermodynamics

The second law of thermodynamics says that the amount of disorder in a thermodynamic system always increases.

Maxwell's Equations | Equations That Changed the World | Abakcus

Maxwell’s Equations

Maxwell's equations were the first major unification of physical forces, showing that electricity and magnetism are intimately interrelated.

Navier-Stokes | Equations That Changed the World | Abakcus

Navier-Stokes

Navier-Stokes is actually Newton’s second law of motion in disguise. This formula provides an accurate way to calculate how fluids move.

Fourier Transform | Equations That Changed the World | Abakcus

Fourier Transform

Fourier transform says any pattern in space and time can be considered a superposition of sinusoidal patterns with different frequencies.

Abakcus is the best curation site for only math and science. We do the hard job and curate the best articles, books, tools, products, videos, and projects.

Categories

About