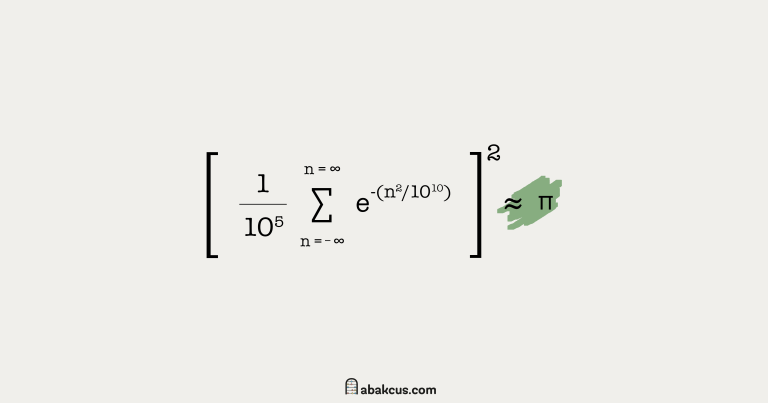
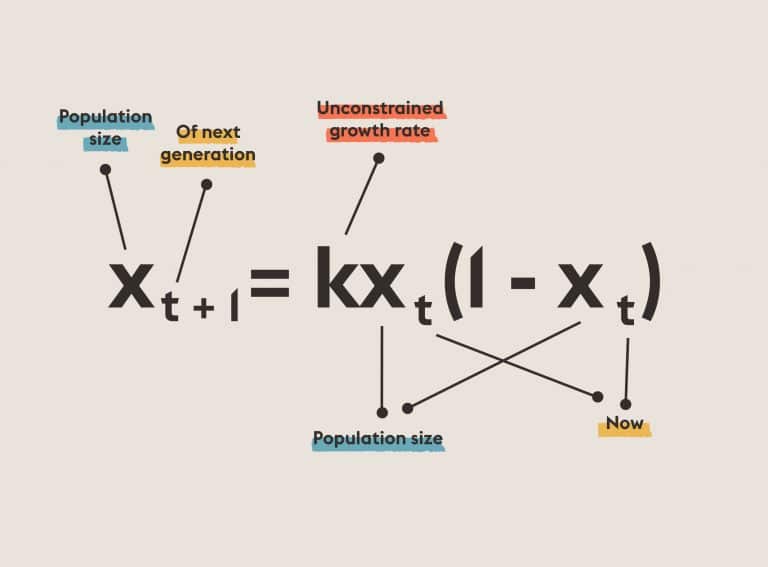
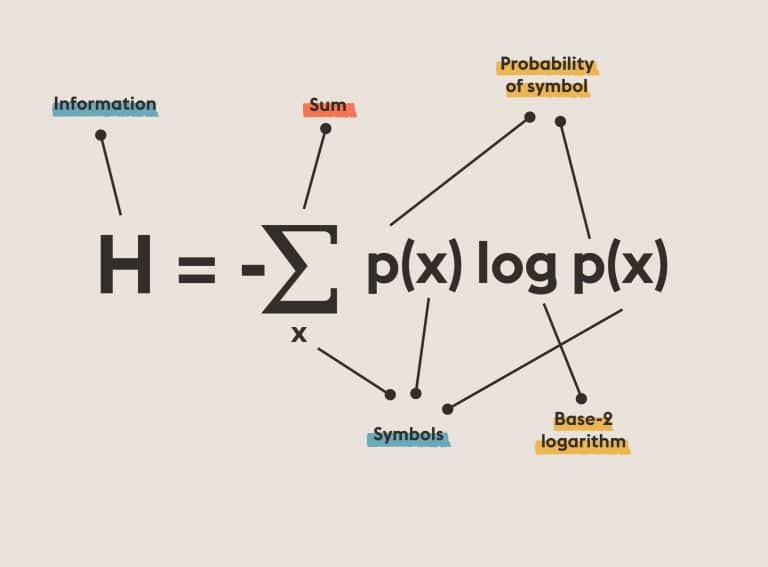
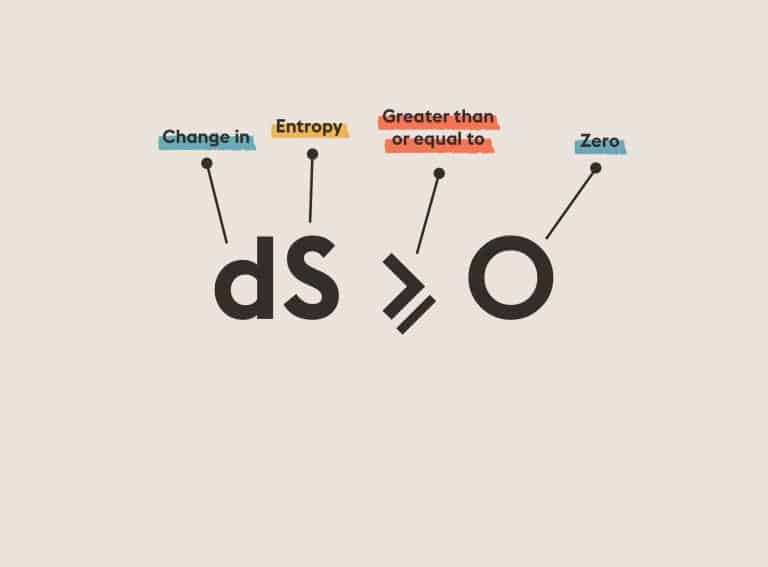
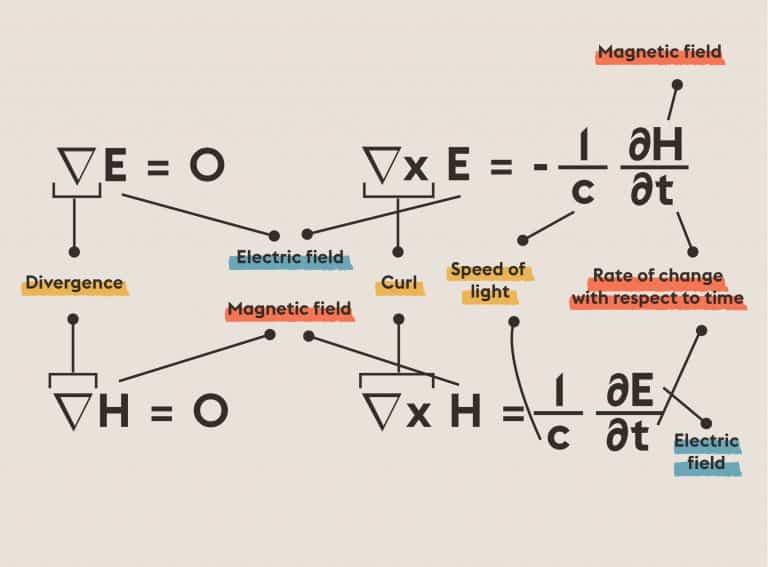
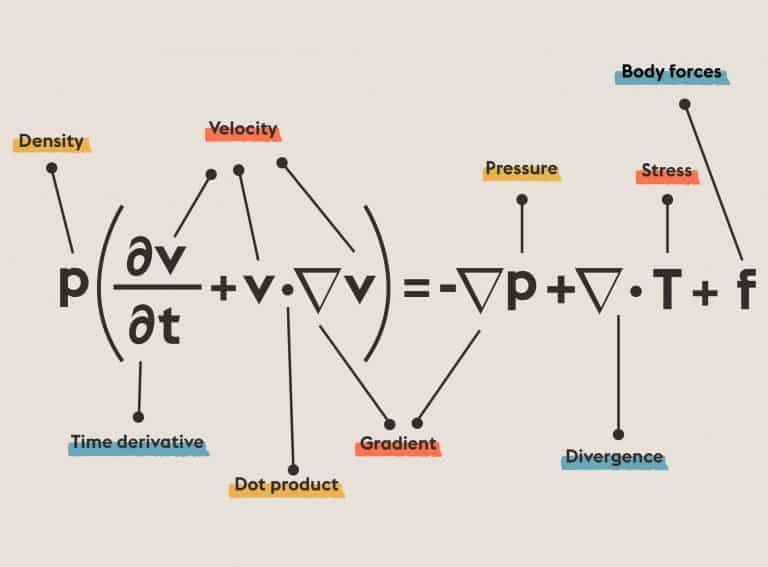
ToHilbert’s Sixteenth Problem: Describe relative positions of ovals originating from a real algebraic curve and as limit cycles of a polynomial vector field on the plane.
Hilbert’s 16th problem is an expansion of grade school graphing questions. An equation of the form ax + by = c is a line; an equation with squared terms is a conic section of some form — parabola, ellipse or hyperbola. Hilbert sought a more general theory of the shapes that higher-degree polynomials could have. So far the question is unresolved, even for polynomials with the relatively small degree of 8.