Hilbert’s Seventh Problem

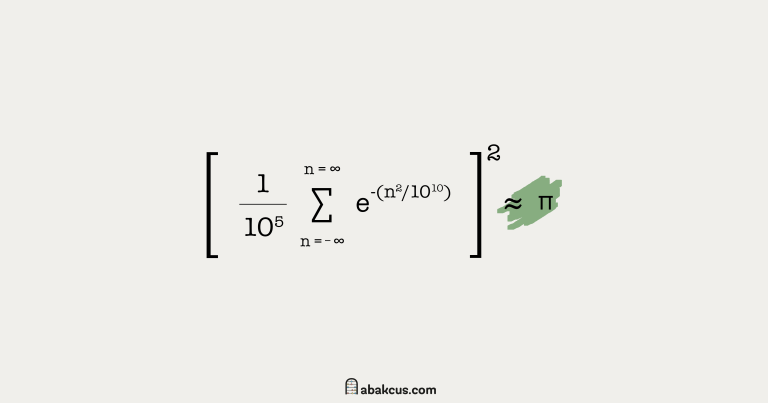
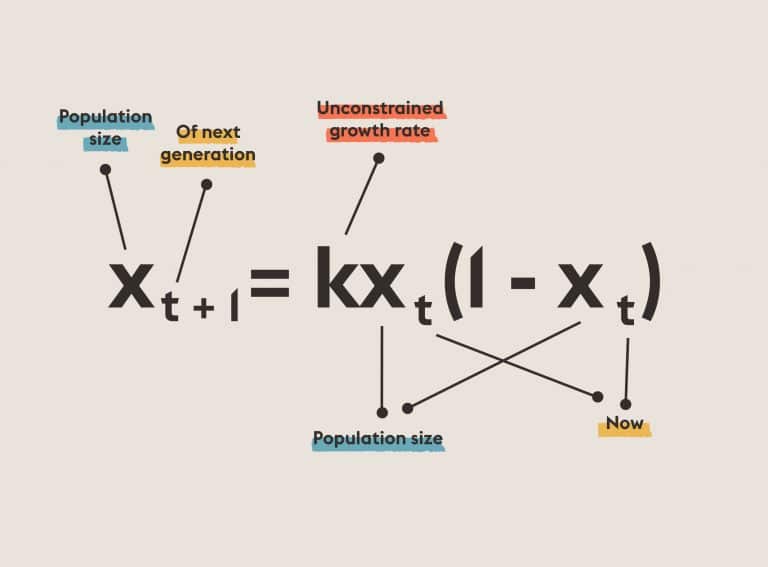
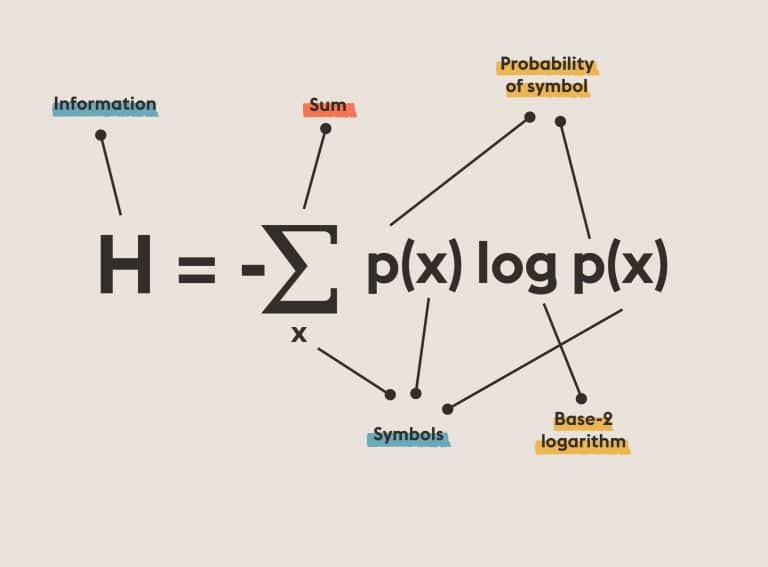
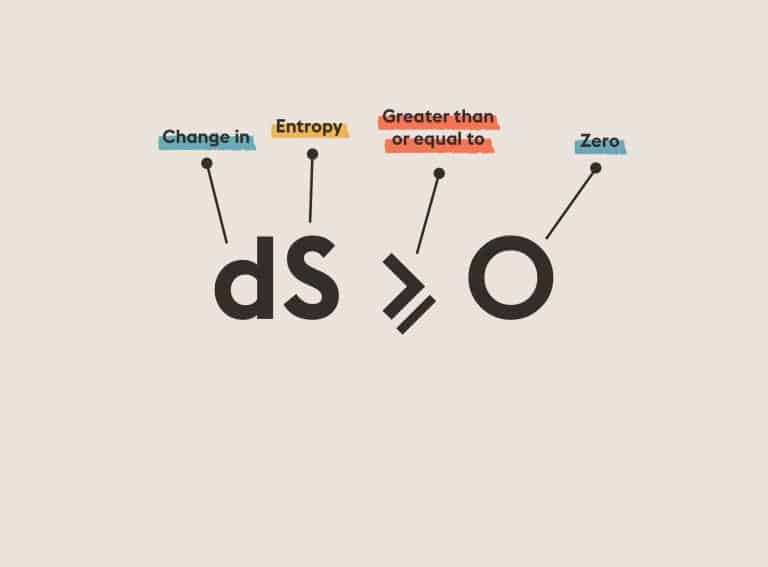
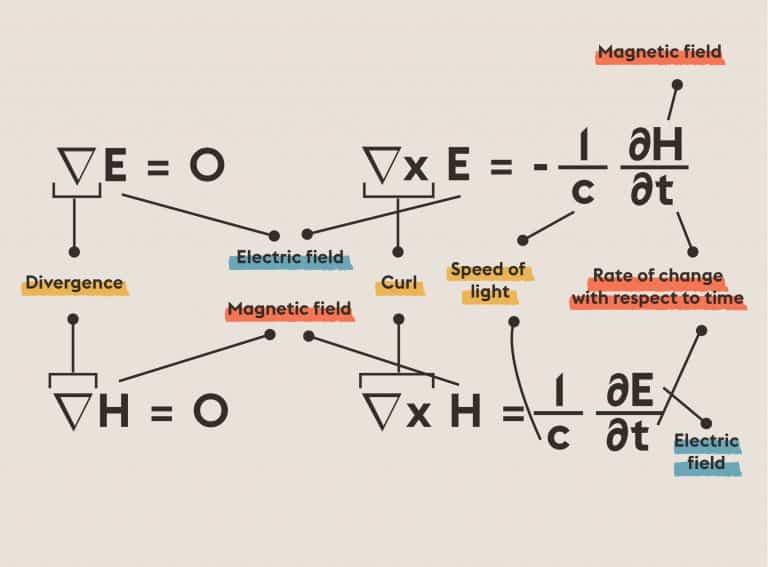
EHilbert’s Seventh Problem: Express a nonnegative rational function as quotient of sums of squares

Some polynomials with inputs in the real numbers always take non-negative values; an easy example is x² + y². Hilbert’s 17th problem asks whether such a polynomial can always be written as the sum of squares of rational functions (a rational function is the quotient of two polynomials). In 1927, Emil Artin solved the question in the affirmative.

Similar Stuff

The Formula to Get 42 Billion Digits of π

While writing "7 Utterly Well-written Math Books About Pi," I found a very interesting math formula that will give you 42 consecutive digits of π accurately but is still wrong.

Black-Scholes Equation

Black-Scholes equation says how the price of financial derivative changes over time, based on the principle that when the price is correct.

Chaos Theory

Chaos theory models how a population of living creatures changes from one generation to the next, when there are limits to the available resources. It is one of the simplest…

Information Theory

Information theory ushered in the age of information. It is basic to today’s digital communications—phones, CDs, DVDs, the Internet.

Schrödinger’s Equation

Schrödinger's equation says that the equation models matter not as a particle but as a wave and describes how such a wave propagates.

Relativity

Einstein's relativity formula says that matter contains energy equal to its mass multiplied by the square of the speed of light.

Second Law of Thermodynamics

The second law of thermodynamics says that the amount of disorder in a thermodynamic system always increases.

Maxwell’s Equations

Maxwell's equations were the first major unification of physical forces, showing that electricity and magnetism are intimately interrelated.

Navier-Stokes

Navier-Stokes is actually Newton’s second law of motion in disguise. This formula provides an accurate way to calculate how fluids move.