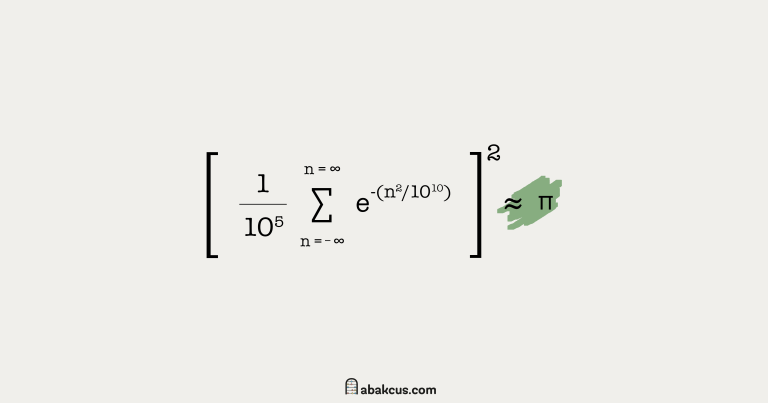
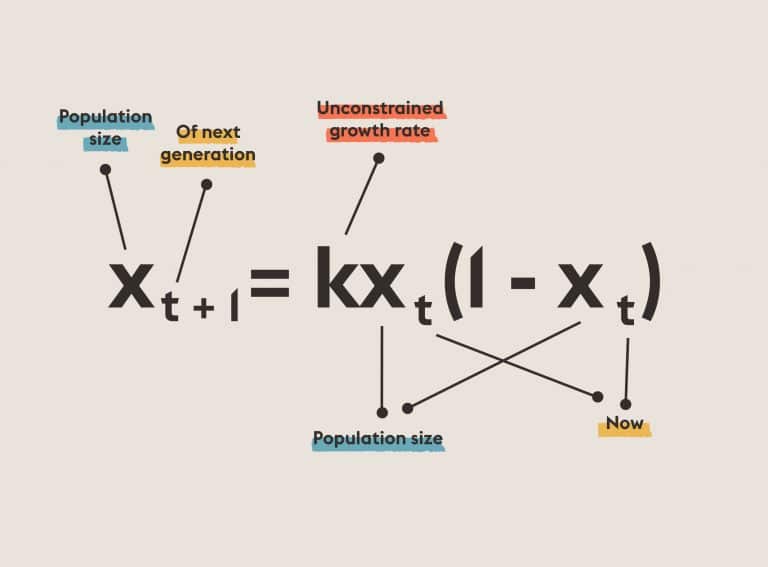
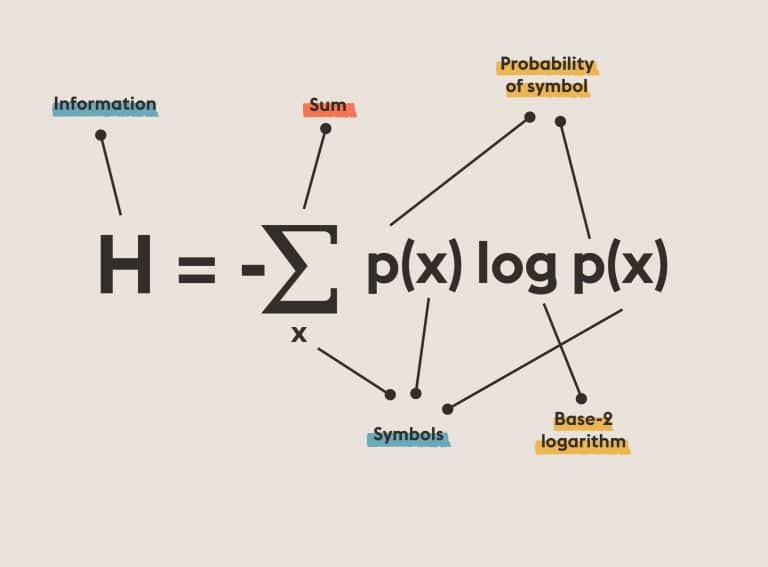
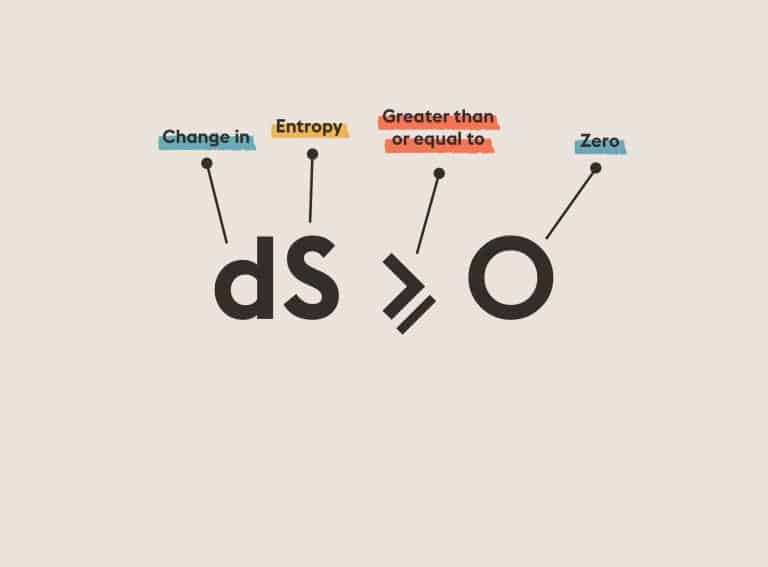
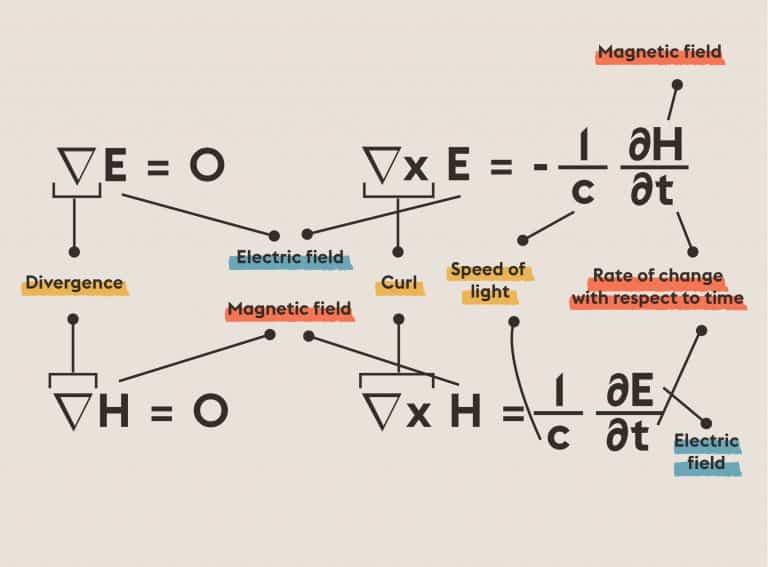
Seventh-Degree Polynomials: Solve 7th degree equation using algebraic (variant: continuous) functions of two parameters.
Hilbert’s 13th problem is about equations of the form x7 + ax3 + bx2 + cx + 1 = 0. He asked whether solutions to these functions can be written as the composition of finitely many two-variable functions. (Hilbert believed they could not be.) In 1957, Andrey Kolmogorov and Vladimir Arnold proved that each continuous function of n variables — including the case in which n = 7 — can be written as a composition of continuous functions of two variables. However, if stricter conditions than mere continuity are imposed on the functions, the question is still open.