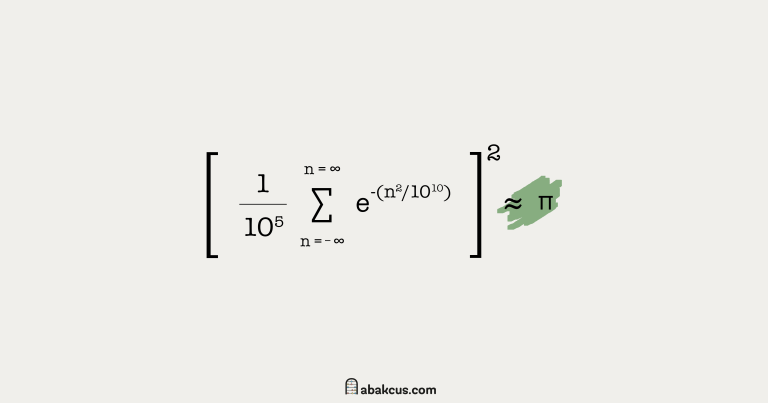
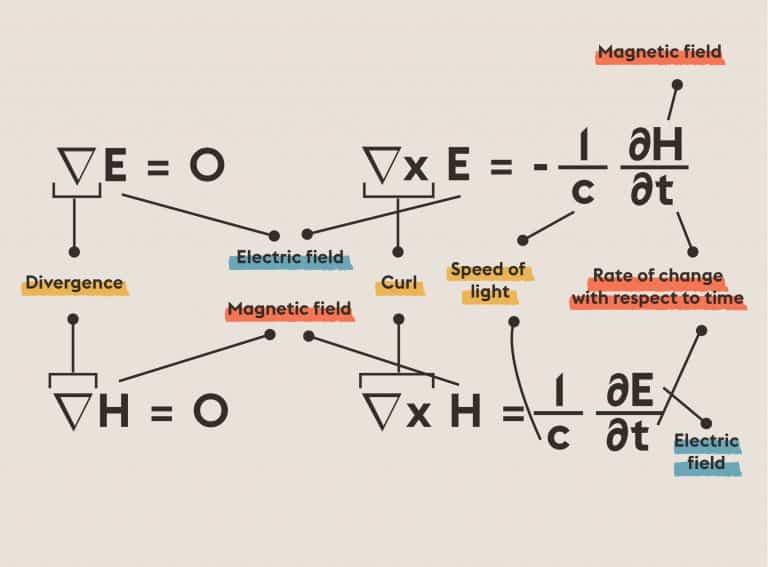
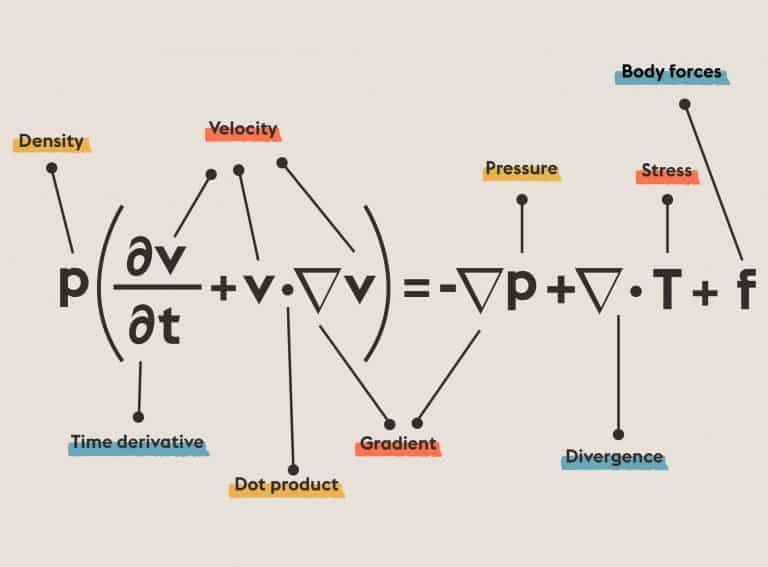
Hilbert’s Eighteenth Problem:
(a) Is there a polyhedron that admits only an anisohedral tiling in three dimensions?
(b) What is the densest sphere packing?
Hilbert’s 18th problem is a collection of several questions in Euclidean geometry. First, for each n, does Euclidean space of dimension n have only a finite number of fundamentally distinct translation-invariant symmetries? In 1910, Ludwig Bieberbach answered this part of the question in the affirmative. Second, in a tiling of the plane by squares, any square can be mapped to any other square. Such a tiling, in any dimension, is called isohedral. This part of the problem concerns the existence of non-isohedral tilings in three-dimensional space. In 1928, Karl Reinhardt found such a tiling. (Later, Heinrich Heesch found a tiling in two-dimensional space; though Hilbert did not say why he did not ask the same question about two-dimensional space; many people assume it is because he did not realize such a tiling could exist there.) Finally, what is the densest way to pack spheres? In 1998, Thomas Hales presented a computer-aided proof showing that the typical configuration in produce stands is indeed optimal.