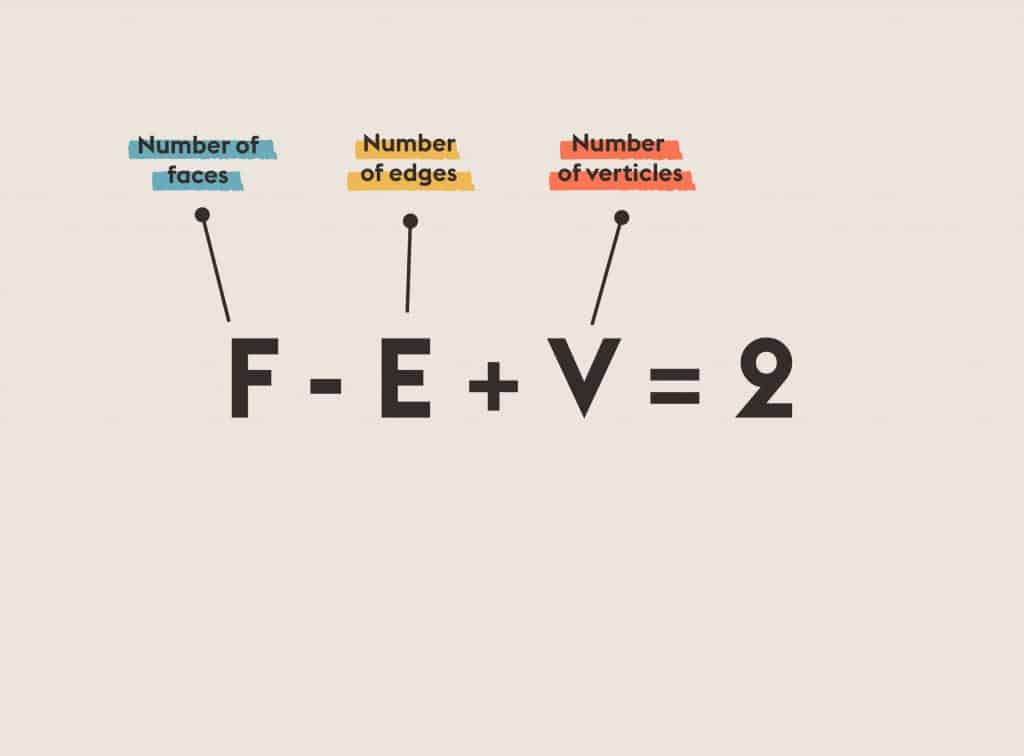
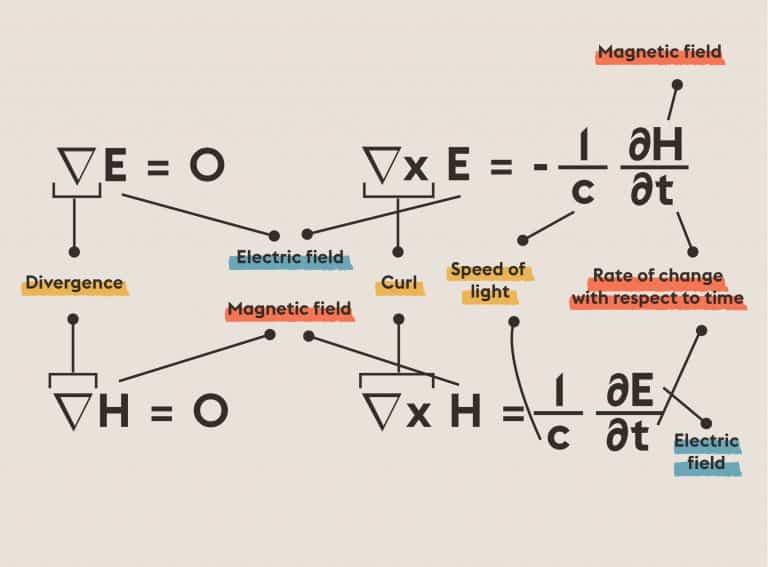
Euler’s formula for polyhedra says that the numbers of faces, edges, and vertices of a solid are not independent but are related in a simple manner. This formula distinguishes between solids with different topologies using the earliest example of a topological invariant. And it paved the way for more general and more powerful techniques, creating a new branch of mathematics. Euler’s formula for polyhedra led us to one of the most important and powerful areas of pure mathematics: topology, which studies geometric properties unchanged by continuous deformations such as surfaces, knots, and links. Moreover, it helps us understand how enzymes act on DNA in a cell and why the motion of celestial bodies can be chaotic.
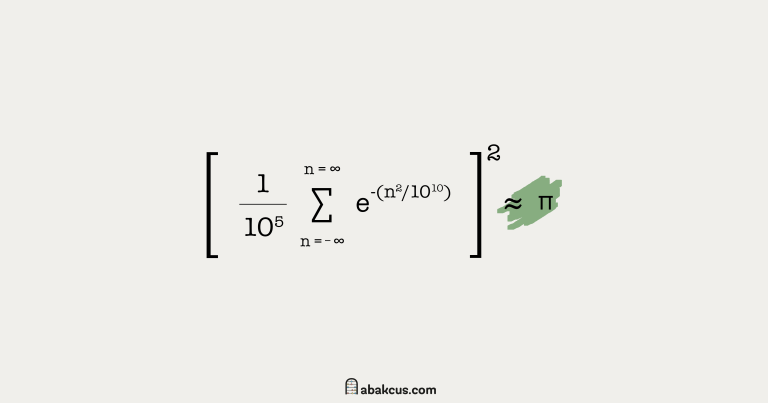
The Formula to Get 42 Billion Digits of π
While writing "7 Utterly Well-written Math Books About Pi," I found a very interesting math formula that will give you 42 consecutive digits of π accurately but is still wrong.