When you gaze out at the night sky, space seems to extend forever in all directions. That’s our mental model for the universe, but it’s not necessarily correct. There was a time, after all, when everyone thought the Earth was flat, because our planet’s curvature was too subtle to detect and a spherical Earth was unfathomable.
Today, we know the Earth is shaped like a sphere. But most of us give little thought to the shape of the universe. Just as the sphere offered an alternative to a flat Earth, other three-dimensional shapes offer alternatives to “ordinary” infinite space.
We can ask two separate but interrelated questions about the shape of the universe. One is about its geometry: the fine-grained local measurements of things like angles and areas. The other is about its topology: how these local pieces are stitched together into an overarching shape.
Cosmological evidence suggests that the part of the universe we can see is smooth and homogeneous, at least approximately. The local fabric of space looks much the same at every point and in every direction. Only three geometries fit this description: flat, spherical and hyperbolic. Let’s explore these geometries, some topological considerations, and what the cosmological evidence says about which shapes best describe our universe.
Flat Geometry
This is the geometry we learned in school. The angles of a triangle add up to 180 degrees, and the area of a circle is πr2. The simplest example of a flat three-dimensional shape is ordinary infinite space — what mathematicians call Euclidean space — but there are other flat shapes to consider too.
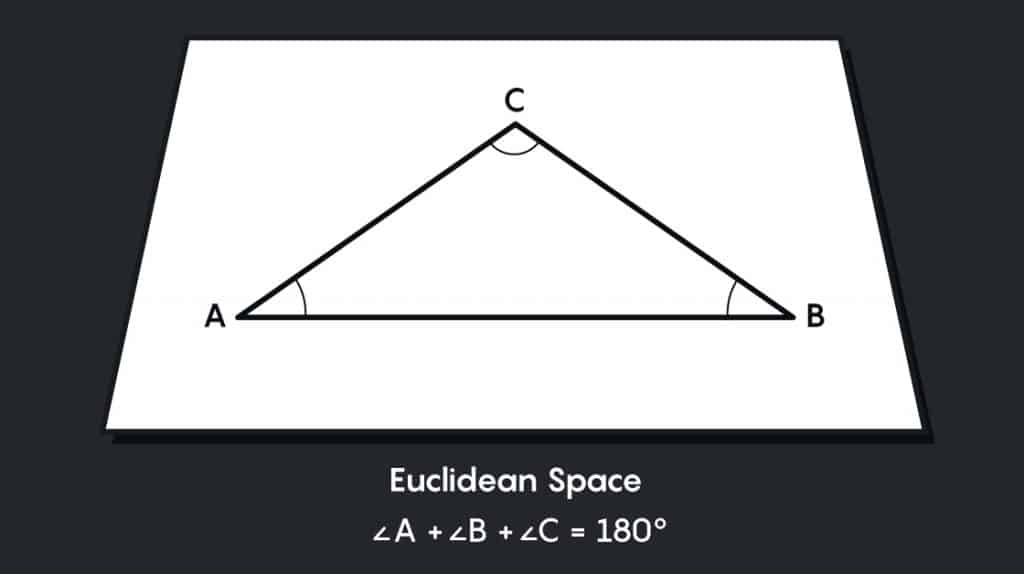
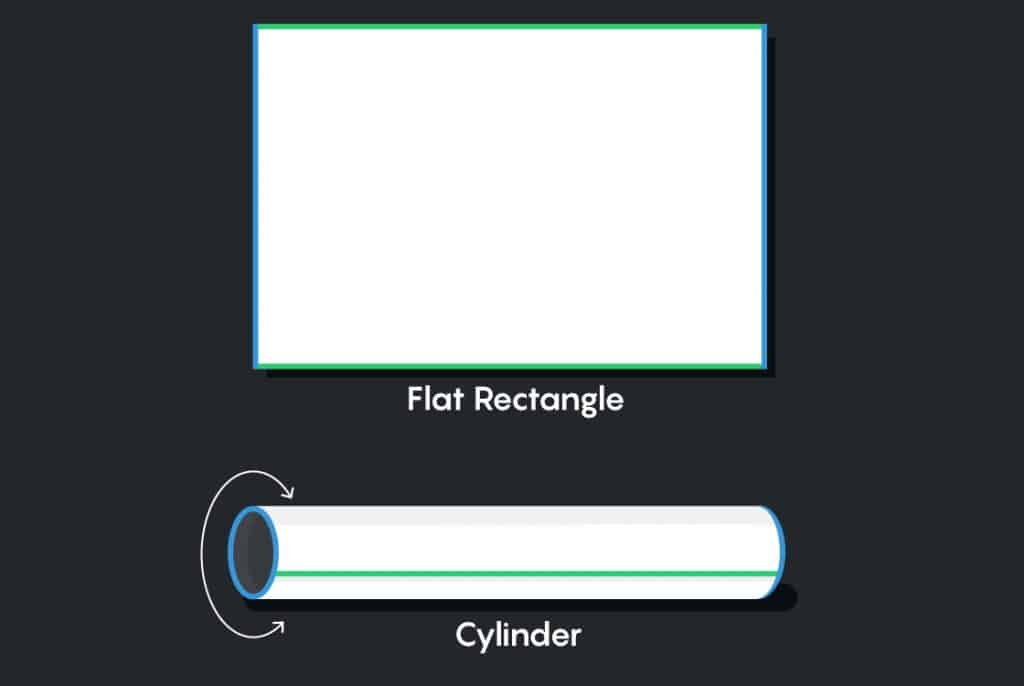
These shapes are harder to visualize, but we can build some intuition by thinking in two dimensions instead of three. In addition to the ordinary Euclidean plane, we can create other flat shapes by cutting out some piece of the plane and taping its edges together. For instance, suppose we cut out a rectangular piece of paper and tape its opposite edges. Taping the top and bottom edges gives us a cylinder:
Next, we can tape the right and left edges to get a doughnut (what mathematicians call a torus):
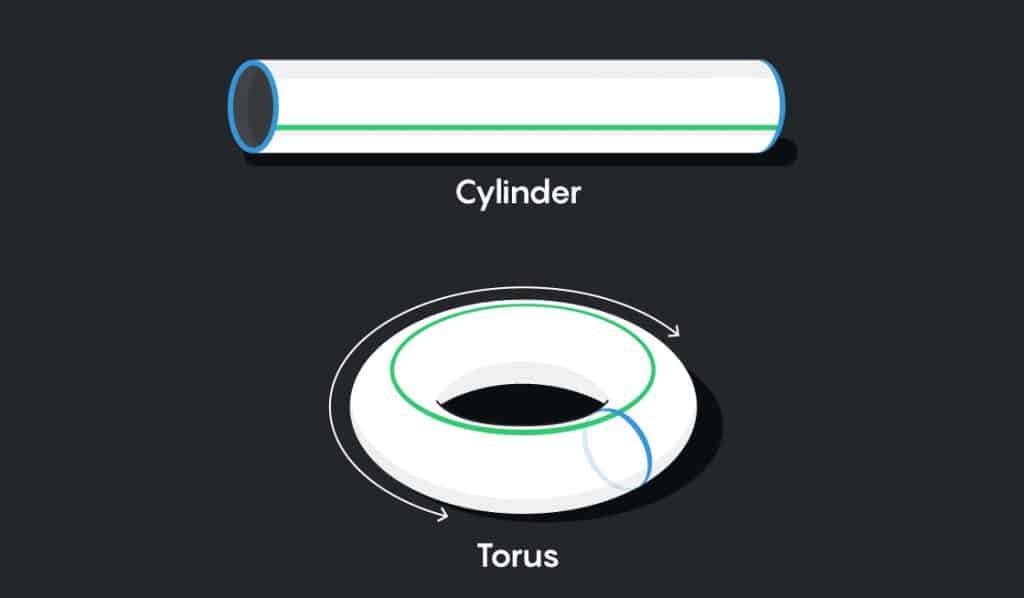
Now, you might be thinking, “This doesn’t look flat to me.” And you’d be right. We cheated a bit in describing how the flat torus works. If you actually tried to make a torus out of a sheet of paper in this way, you’d run into difficulties. Making the cylinder would be easy, but taping the ends of the cylinder wouldn’t work:














