Newton’s three Laws of Tennis control the behavior of racquets and balls in most cases, and Howard Brody’s book The Physics and Technology of Tennis explains these concepts in detail. The following is an overview of a few interesting subjects to give you an idea of how physics relates to sports and daily objects.
1. A tennis racquet’s sweet spots
A sweet spot exists in a tennis racquet, just as it does in a baseball or cricket bat. When a ball hits the sweet spot, the force transferred to the hand is so minimal that the player is nearly completely oblivious of the hit. The player will feel some jarring and vibration of the handle if the ball hits far away from the sweet spot. A vibrating node near the center of the strings is the sweet spot. Another potential sweet spot is the percussion center (COP). These, as well as a few other key areas on a racquet, are depicted below.

The sweet spot does not, according to common belief, correspond to the position at which the ball rebounds at maximum speed or the point at which the force on the hand is zero. Three distinct motions of the handle, namely rotation, translation, and vibration, produce forces on the hand. When a ball contacts the vibration node, the vibrational component is absent. The torque exerted on the hand by the rotational component of the racquet head’s recoil causes it to rotate around an axis via the wrist. As an outcome, a force is always applied to the upper part of the hand, while a force is always applied to the lower part of the hand in the opposite direction.
When the racquet is freely suspended, the COP depicted in the diagram is close to the node point, but it shifts into the throat area when the racquet is gripped in hand. As a result, the COP depicted in the diagram is NOT the sweet spot that players discuss.
2. Nodes of Vibration
The first two vibration nodes of a tennis racquet suspended freely are shown here. Because the center of mass of a racquet is at the center of the racquet, it behaves like a uniform beam in this regard, despite its round head. For a somewhat flexible frame, the fundamental node has a frequency of around 100 Hz, whereas, for a stiff frame, it has a frequency of approximately 180 Hz. The handle has two nodes, one at the center of the strings and the other in the handle. If you grip the handle lightly at the node in the handle, close to your ear, and then strike the frame or strings, you may easily hear this vibration. Using this method, the vibration node on the strings may be easily located. The frame vibrations (but not the string vibrations) are considerably damped if you grasp the handle firmly.
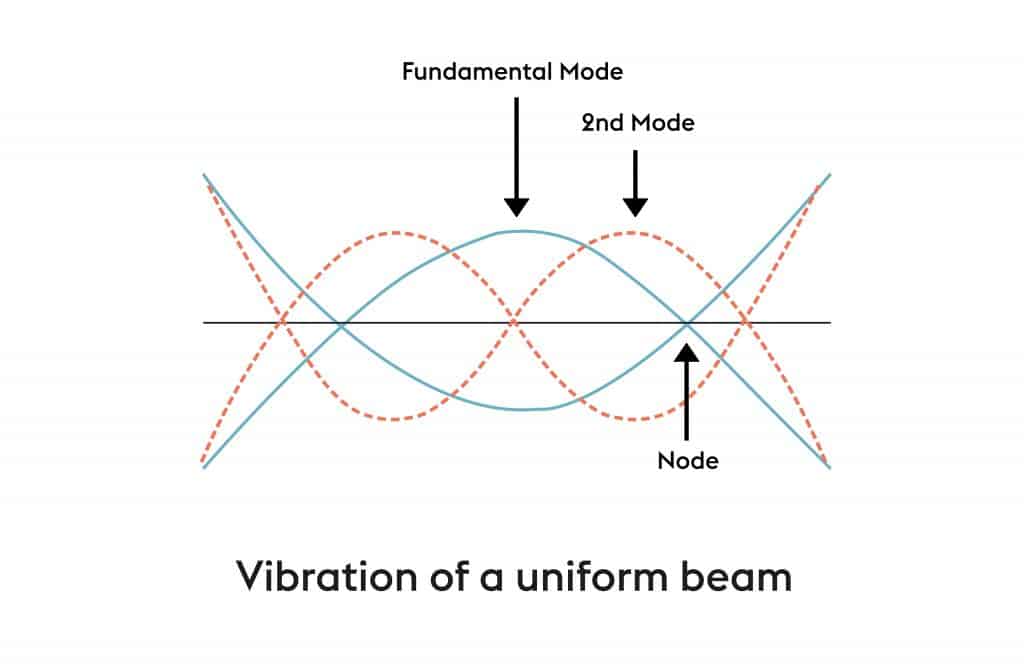
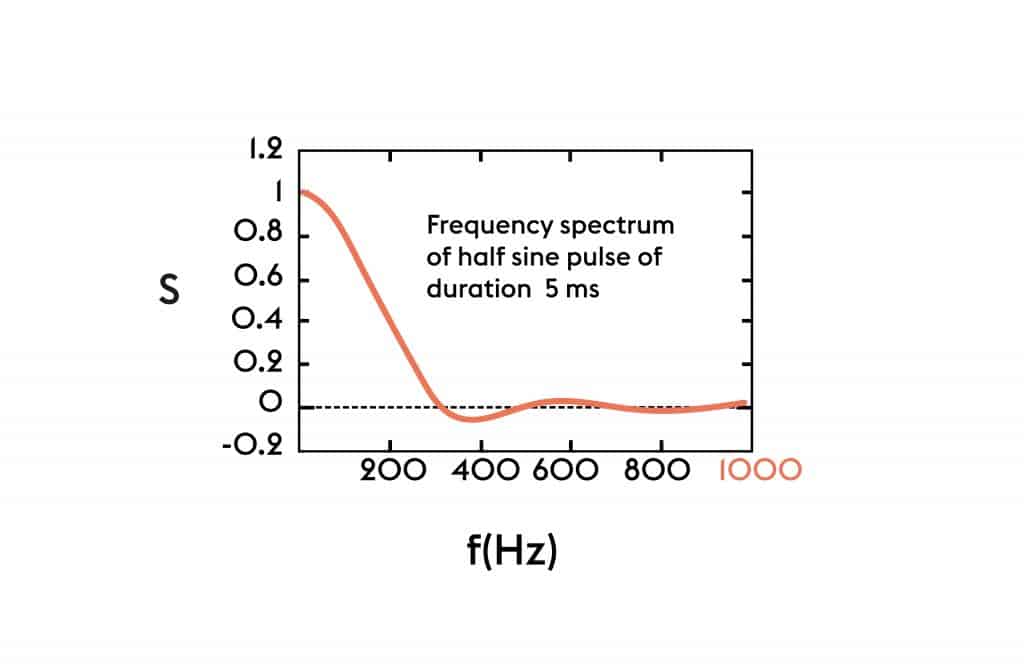
The frequency of the following node, given a homogenous beam, is 2.75 times the fundamental frequency. Because the ball’s impact duration, T, on the strings is roughly 5 ms, it is not thrilled with any considerable amplitude. This pulse’s frequency spectrum, roughly a half-sine waveform, peaks at zero frequency and falls to zero at f = 1.5/T = 300 Hz, close to the second node frequency. Because the strings are not as well damped as the frame, the impact will still cause string vibrations at around 500 Hz.
A racquet’s vibration usually is too small to perceive with the naked eye, but a cardboard racquet vibrates in the same way and reveals the vibration nodes (see photo below). At a frequency of around 30 Hz, the top end was vibrated back and forth by roughly 1 mm. The nodes in the frame and the two strings can be seen clearly.
The stiffness of the frame determines the vibration frequency of a racquet. This is one way to tell if you’re playing with a stiff or flexible racquet. A firm racquet vibrates at a frequency of 180 Hz or higher, and a flexible racquet vibrates at a frequency of less than 140 Hz. For frequencies of 120, 140, 160, 180, 200, and 220 Hz, QuickTime sound files for a racquet held near the ear and tapped with a finger or a ball near the tip are connected. These sounds are too low in frequency to be heard clearly using a computer’s internal speakers. You will only hear a few mechanical clicks when the racquet is struck. The bass response of internal speakers is frequently non-existent. External speakers must be connected with fresh batteries if they are battery-operated.
Hitting a tennis ball on the court is the finest method to feel a racquet vibrate. What exactly do you “feel”? Is it pleasant or unpleasant? What makes racquets feel so different? Does a $400 racquet feel significantly better than a $100 racquet, and if so, in what ways? These are not simple questions to respond to. I’ve never heard a good explanation or description in terms of the mechanics of feeling. Players claim that certain racquets feel more powerful than others, but how can they tell unless they monitor ball speed, which they don’t?
Is it possible to distinguish between a 140 Hz and a 160 Hz vibration? Placing your palm on the speaker used to play the sound files is one approach to test this. Using an external speaker instead of your computer’s built-in speaker will assist. When you hit the racquet, you may feel a thud because the vibration’s variation in amplitude (or size) is easy to detect. High frequencies tickle my hand more than low frequencies, mainly when the sensitive area of my palm rests gently on the speaker.
3. Percussion Center
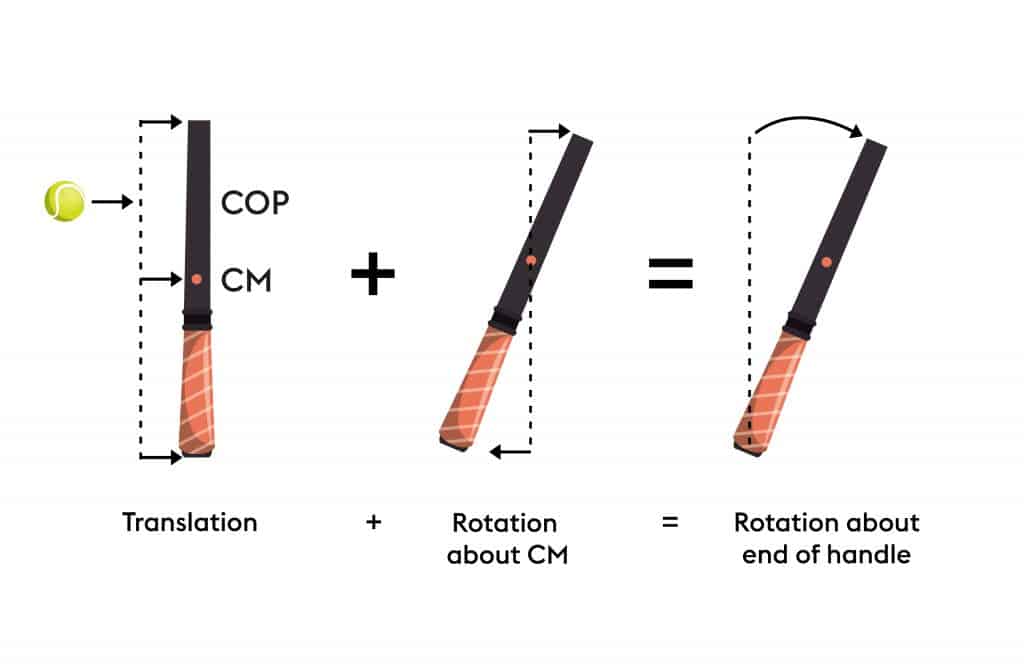
Consider a racquet suspended from the ceiling by a long piece of thread or balanced vertically on the end of the handle. When a ball hits the racquet’s center of mass (CM), the racquet recoils at a speed of V. The racquet will recoil at the same V rate in all areas. If the ball strikes the strings at any other position, the racquet will rebound and revolve around its CM. Due to recoil, the entire racquet travels away from the ball at V1, whereas the handle moves towards the ball at V2 due to racquet rotation. If V1 = V2 at any point on the handle, that point would remain fixed as the rest of the racquet rotates around it, as shown in the diagram below.
With respect to the impact point, the axis of rotation is called the conjugate point, and the impact point is called the center of percussion (COP) for that particular axis of rotation. The axis and the COP form a pair of conjugate points. The axis of rotation for an impact near the racquet’s tip is about halfway between the end of the handle and the CM. The axis of rotation for a collision at the racquet’s throat is beyond the handle’s end.
Consider a racquet supported by a rod that passes through a hole drilled in the handle, allowing the racquet to freely rotate around this axis when a ball strikes the strings. Unless the ball hits the COP, the handle will exert a force on the axis when it hits the strings. As a result, the COP is frequently referred to as a “second sweet spot” because the force on the hand for a collision at the COP should be zero. On the other hand, the hand adds around 500 grams to the handle and moves the COP closer to the racquet’s throat area. The details of this effect may be found in an article published in the American Journal of Physics, which you can download here.
4. A Tennis Racquet’s Dead Spot
Clamp the end of the handle on a table and press down on it with your hand so that the rest of the racquet hangs over the table’s edge. Then, at various spots along the strings, drop the ball. The greatest place for the ball to bounce is around the throat. Near the tip, there is a region where the ball does not bounce at all. That’s where the dead zone is. The racquet receives all of the energy from the ball at the dead spot, and the racquet does not return any energy to the ball. The reason for this is that at that instant, the racquet’s effective mass is equal to the ball’s mass. The effective mass is equal to the ratio of force to acceleration at that position (F = ma, hence m = F/a). When a mass m ball collides with another mass m ball at rest, the incident ball stops dead and transfers all its energy to the other ball.
Similarly, if a moving racquet hits a stationary ball at the dead spot, the ball receives all of the racquet’s rotational energy. The dead spot is a nice position to hit the ball when serving. On the other hand, the dead spot is the worst position to hit the ball while returning a quick serve. This is the optimal place because the ball bounces best near the racquet’s throat.
5. Tennis Balls
When a tennis ball is dropped from a height of 100 inches onto a concrete slab, the regulations state that it must bounce to a height of 53 to 58 inches. It’s difficult to predict what will happen in actual play, but dropping the ball onto the strings with the head clamped is a decent test (eg, by placing the racquet on the floor and stepping on the handle near the head). The ball will bounce to a height of around 0.70 meters when dropped from a height of 1 meter. When the ball is dropped on concrete, it loses approximately 45 percent of its energy but only 30 percent when dropped on the strings. The strings absorb some of the impact energy and then return practically all of it to the ball. The ball’s compression determines how much energy it loses. It shrinks by roughly 6 mm when dropped from 100 inches onto concrete. It compresses by around 3 mm when dropped on the strings. When the ball expands back to its original shape, the more the compression, the more energy is lost. That means the energy loss is significantly larger at high impact speeds when the ball compresses more. Furthermore, if the ball’s energy or compression is increased, the fraction of the ball’s lost energy increases as well.
6. Spin the Ball
The amount of spin that players can give to the ball dominates the current game of tennis. Players could hit with greater topspin because the ball was less likely to clip the frame when switching from small 9-inch heads in wood racquets to large 10.5-inch heads in graphite racquets. Because balls hit with topspin fall down more sharply onto the court after clearing the net, players could hit the ball harder. Players generated more topspin by striking the ball harder, allowing them to strike the ball even harder. Current tennis is played at a significantly faster pace than wood racquets, not because modern racquets or players are more powerful, but because racquet heads are now an inch or two larger, allowing players to hit the ball with much more topspin.
Players have learned to swing up at the ball and tilt the racquet head forward to extract as much topspin as possible from a stroke. This allows a ball that has come off the court with topspin to be returned. To get this result, the spin direction must be reversed. Two QuickTime movie files, one by Howard Brody and Federer, are included to demonstrate how this is done. The physics of each shot is identical, except that Federer’s approach is more graceful. The ball sits on the strings for roughly 5ms and is observed for 4 or 5 frames, indicating that Federer’s clip was shot at around 1000 frames per second.
The quantity of spin is determined by several elements, including the incident ball’s speed, spin, angle, the racquet’s speed, approach angle, tilt, and the string type. Because the racquet does not brush against the rear of the ball when the ball rises at the same rate as the racquet, no topspin is generated, as illustrated in this movie clip. The player will generate more topspin if he smashes the ball while it is dropping rather than when the approaching ball rises, as evidenced by this result.
http://twu.tennis-warehouse.com/learning center/spinexperiment.php has detailed measurements and calculations of ball spin off various strings, as well as movie clips demonstrating the results.














