How to Use Math to Dominate at Monopoly?

Monopoly is one of the classic American games. It’s played among close friends, loved ones, and trusted business partners. It’s also one of the few times in life where it’s perfectly acceptable to want to systematically annihilate and crush the friends, as mentioned earlier, loved ones and partners. Well, we’re here to help.

Monopoly has a major element of chance in it, and the best part about games of chance is that people with Microsoft Excel can solve them. We broke down the must-know math behind Monopoly as well as several lessons you can take away from what truly is The Most Dangerous Game. 

In this article, we’ll teach you such concepts as:

• The most important properties in the game
• The crucial “axis” will change the way you think about the shape of the board.
• Where you should invest.
• How to make moves so that your opponent will keep landing on your properties.

Monopoly has an element of chance, but it can still be predicted. 

• Monopoly is a game of skill and chance 
• The thing with games of chance is that we have the mathematical ability to break them down finally. 
• Here, we’ll talk about how to increase your skill in Monopoly. 

Let’s start with the most basic probability in Monopoly: Rolling the dice. 

All of the randomness in Monopoly is derived from the dice roll. The most fundamental element of chance in the game of Monopoly is the dice roll. So, let’s build-up to a model of the Monopoly board starting here. 

Here’s the probability of where you’ll land after rolling two dice from the starting position.

So right off the bat, here’s what we know; on your first roll, you have the highest chance of landing on chance. You also have comparatively higher probabilities of landing on Oriental or Vermont. You also have a greater than one in ten chance of landing on the Reading Railroad or Connecticut. 

But the thing is, rolling doubles changes that distribution a lot.

• In Monopoly, when you roll a set of doubles, you get to move again. 
• The previous graph is an excellent calculator where someone will and on their next roll. 
• If we want to find out where someone will end their turn — which will help us figure out other probabilities — we need to factor in doubles. 

Here’s how often you roll a double:

Rolling doubles can be decisive. It’s technically possible (though highly improbable) to get to the Short Line railroad by dice alone on your first turn. The probability is 0.00021%.

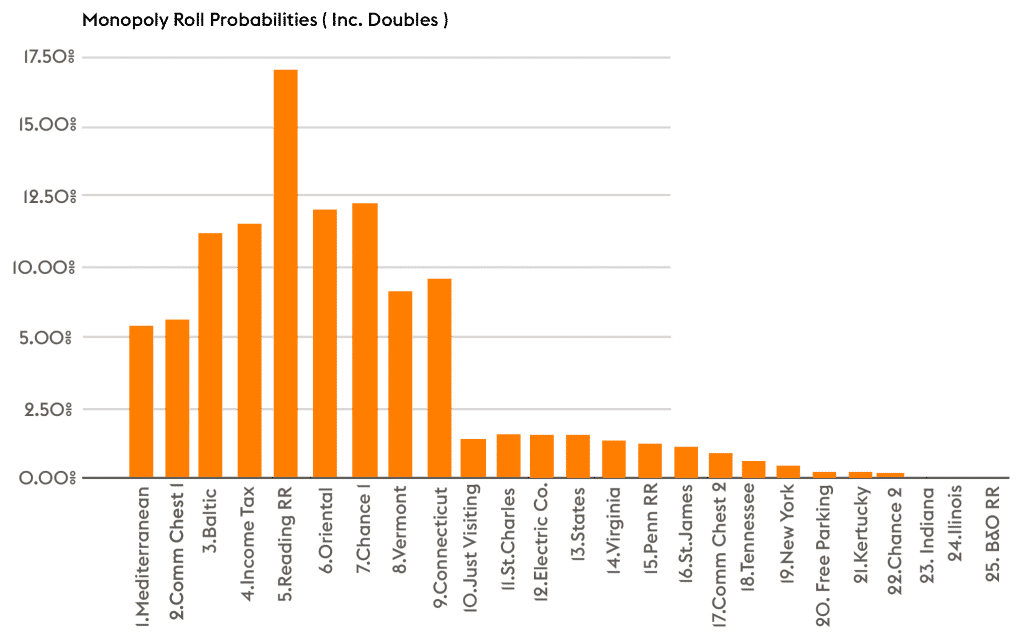
Theoretically, this could go on indefinitely. Conveniently, Monopoly has the “speeding” rule. This means that you go to jail after rolling three doubles. The problem gets exponentially harder after calculating the second roll; the next chart only factors in two rolls or 97% of all cases.

Here are the probabilities of ending on a space on the first turn of the game:

Already, we have a few tactical pointers. Let’s say you want to build a few houses, and you see your opponent coming up on some of your properties. Your opponent will most likely roll a seven and is also very likely to roll a five, six, eight, or nine. ‘When you can, build houses 5, 6, 7, 8, or 9 spaces ahead of adversaries. 

Of course, winning Monopoly is not that easy. Unfortunately, Monopoly isn’t only simple dice rolls. The good news is, that’s precisely why it’s so fun! If we only dice rolls around a circle, each space would be equally likely, which is really dull. 

Specific spaces are more likely to get hit than others. Three things mess with the probabilities of the Monopoly board. 

• Chance Cards 
• Community Chest Cards 
• Go To Jail 

By understanding how these change the board, we can see how different spaces become more or less likely. 

Using Change Cards to Your Statistical Advantage

Understanding how Chance Cards change the board is crucial to understanding the Monopoly. In Monopoly, when you land on the Chance space, you draw one of sixteen Chance cards. Chance cards tell you one of five things: 

• You can get out of jail free (1/16) 
• You collect money (3/16) 
• You advance somewhere on the board. (8/16) 
• You pay money (3/16) 
• You go to jail. Directly. (1/16) 

Here’s how chance cards dramatically change the game:

• In 9 of the 1.6 chance cards, you’re transported from one of the three chance spaces to another space. This has an effect on the different weights of specific areas on the board. The next paragraph looks at what happens. 

Here are the places Chance can send you:

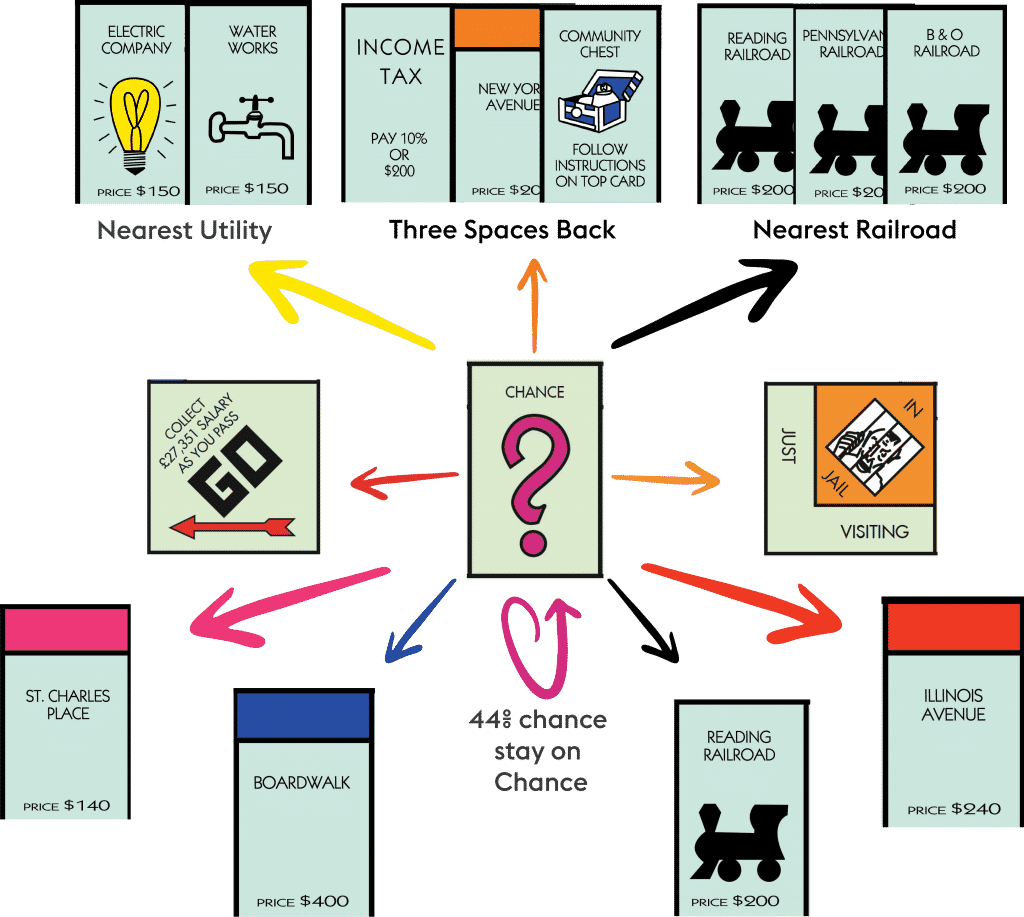
Here’s where they send you geographically:

This leads to some skewing in the board. You’ll notice that the Chance Cards send you to the first and second rows much more frequently than sending you to the third and fourth rows. This increases the frequency you land on specific spaces and decreases the frequency you land on others. We’ll get to more on this soon.

Using Community Chest to Your Statistical Advantage

Another crucial card is the Community Chest space. In Monopoly, when you land on the Community Chest space, you draw one of 16 cards. Community Chest cards tell you one of five things: 

• You can get out of jail free (1/16) 
• You collect money (9/16) 
• You advance somewhere on the board. (416) 
• You pay money (4/16) 
• You go to jail. Directly. (1/16) 

You can mathematically anticipate what will happen when you land on either Chance or Community Chest.

Community Chest is much easier to understand when it comes to travel.

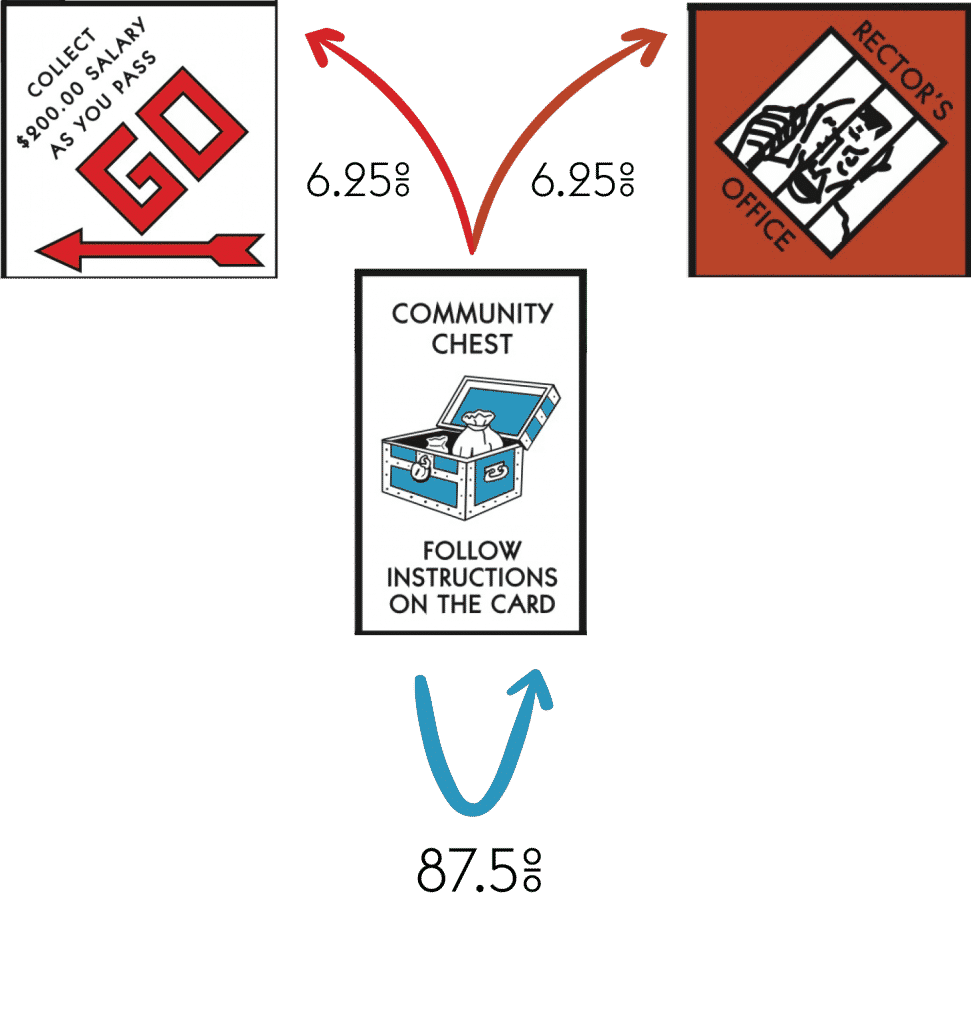
Thinking about how to exploit the effects of Chance and Community Chest will make you a better Monopoly player. You should buy the properties that Chance sends you to —the Railroads, New York Ave, St. Charles Place, Illinois Ave, and Boardwalk. It would help if you also bought properties neighboring these areas.

Why Jail Is the Most Crucial Space on the Whole Board?

Jail is beyond crucial for understanding the complexities of Monopoly. By far, one of the biggest things that change the frequency people hit certain spaces is jail. You can go to jail for one of four reasons: 

• Roll 3 doubles in a row, “Speeding.” 
• Go To Jail space.
• Go To Jail Chance card.
• Go To Jail Community Chest Card.

Here’s how jail works: Once you go to jail — whatever your grievous crime maybe — you have a couple of ways of getting out. 

1. You can use or buy a Get out of Jail Free card.
2. Pay at the start of either of your next two turns. 
3. Throw the die and get doubles on any of your next three turns 4. After a third failure to roll doubles, you have to pay $50. 

Don’t want to spend $50? The probability you roll out of jail within three rolls is 42%.

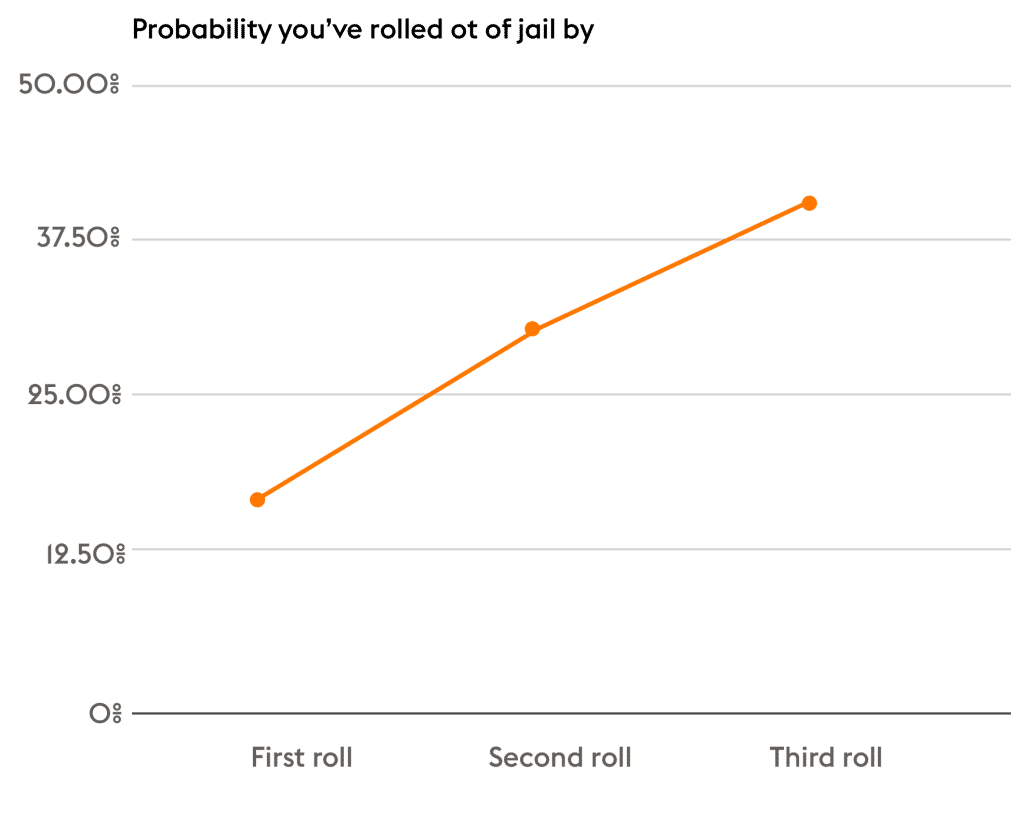
Why does jail matter? Every space that comes after jail gets landed on more frequently than other areas because Jail serves as a sink. People get pulled from the rest of the board and emerge from Jail. Take a look at the next paragraph to see why. 

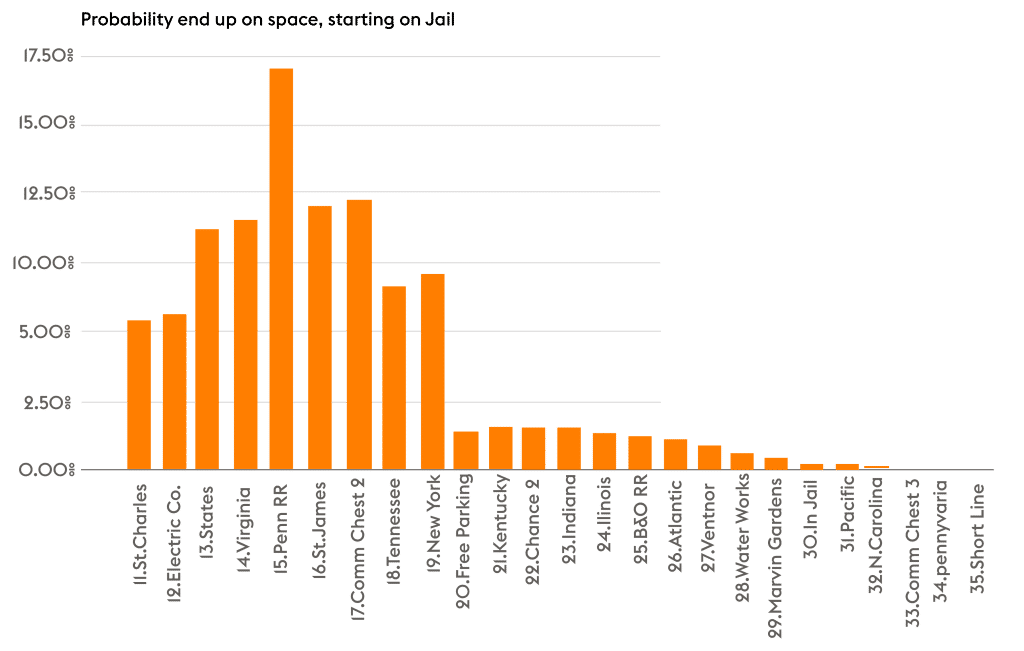
Because so many spaces send people to the Jail/Just Visiting space, it’s the board’s axis. The rolls people have directly exiting Jail matter even more than Go.

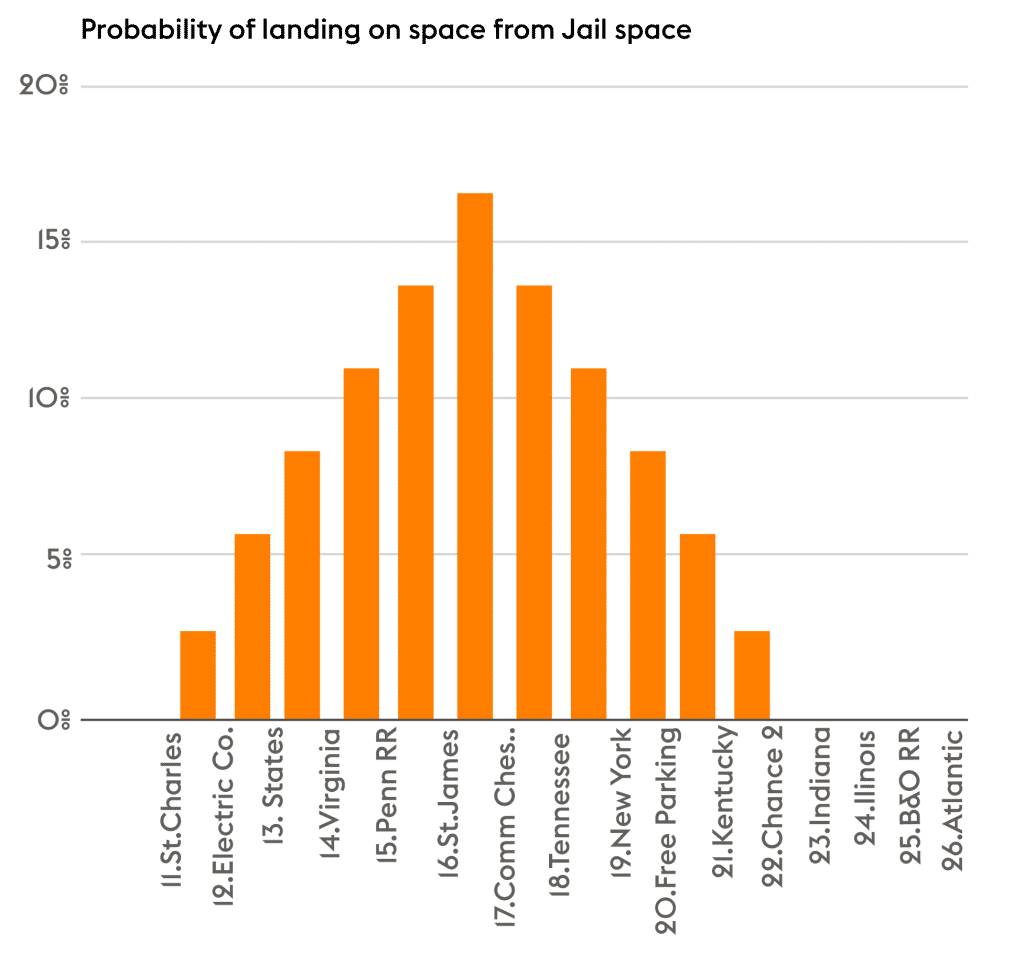
Look at this chart from earlier shifted to start from Jail.  The Purple, Orange, and Red properties have critical strategic importance. 

People go to jail for speeding a lot more often than you’d expect too. The probability of someone rolling three doubles in a row is 0.4%. However, when you look at how many times people roll the dice in a game of Monopoly, that becomes pretty plausible throughout the game. There’s a 20% chance someone goes to jail for speeding in any given 50 player turns.

How to Solve the Statistics of Monopoly?

We now know enough about the board to figure out the probability of any space. We know how to figure out the likelihood of rolling to any other space based on the space you’re currently occupying. We also know how to calculate the probability you get warped to another space by a card. 

Before we go any further in Monopoly, we need to learn one of the game’s most profound mathematical ideas. It’s called a Markov Chain, and here we’ll do an example of the calculation. 

Let’s take a detour to New York City. Let’s say you want to project the eventual population shares of the various boroughs of New York City. You know the number of people exiting each borough to move to another borough for all five regions. Let’s assume for the problem that nobody leaves New York. 

In our Markov Chain example, here’s what we know about Manhattan: 

In any given year, let’s say: 

• 94% of Manhattan residents stay there 
• 3% move to Brooklyn 
• 1.5% move to Queens 
• 1% move to the Bronx 
• o.5% move to Staten Island 

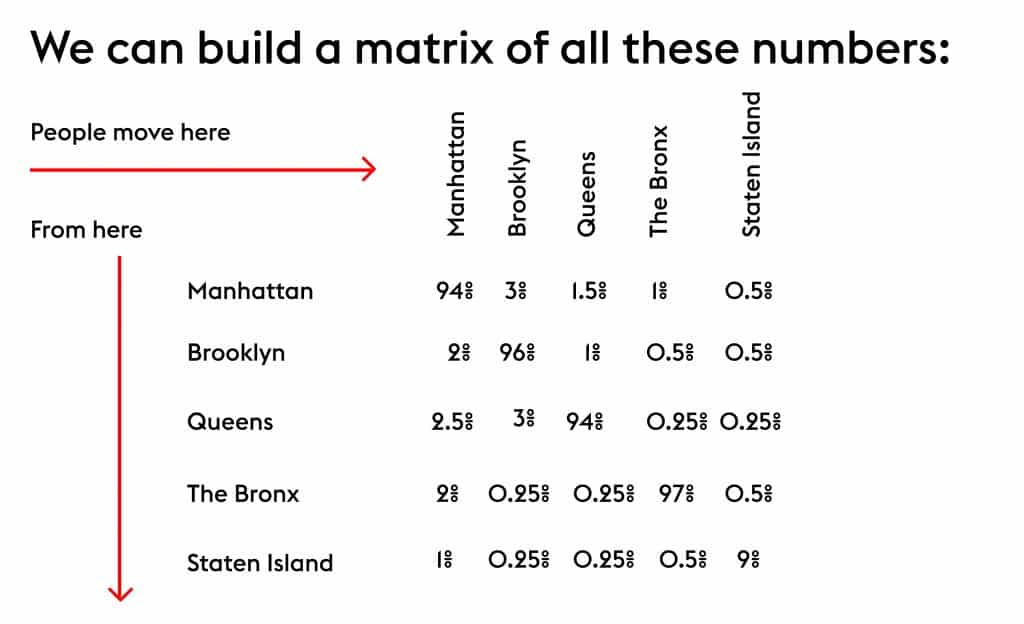
We know these numbers for every borough. 

We can build a matrix of all these numbers. Then we can use a Markov chain to find where people will end up. Let’s call that probability matrix “A.” We make a .a.x5 matrix “B” with a column for each borough. We seed Manhattan with ion citizens and keep everyone else at zero.

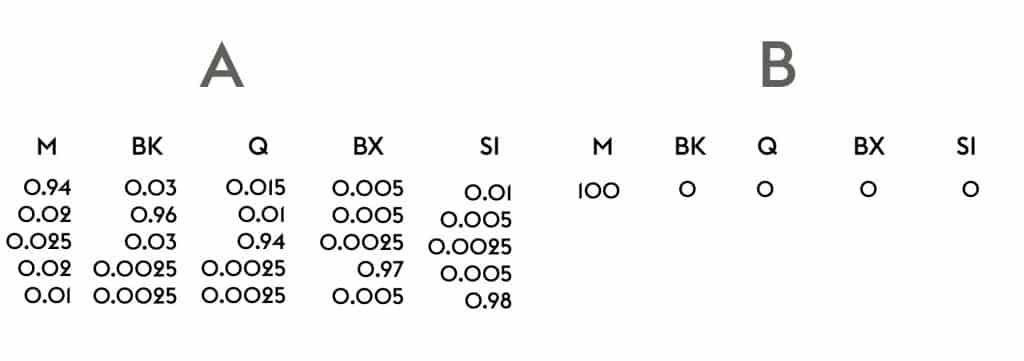
Then we multiply them. We multiply that resulting matrix product by the probability matrix A again.  We do this a hundred times. Eventually, the numbers stop changing. We get a matrix with one number for each borough called a “steady-state probability matrix.” 

By the end of it, we can forecast the long-term breakdown of NYC. 

Knowing how many people move from each borough to every other borough, we learn: 

• 22.8% will live in Manhattan 
• 28.5% will live in Brooklyn
• 12.0% will live in Queens 
• 13.4% will live in the Bronx 
• 23.3% will live in Staten Island

So why am I telling you this? 

We can do the same thing for the Monopoly board! We can make a 40×40 probability matrix. Each row and column represents a space. Each entry will be the probability a person moves from one space o another in a given roll. We factor in the dice probability, Chance and Community Chest probabilities, and how you can go to jail. 

Then, just like we did with the NYC example, we can figure out the steady-state probability someone lands on any space.

THE PROBABILITY SOMEONE ENDS A TURN ON ANY SPACE ON THE BOARD 

So now, let’s look at the state of the board. The next paragraph will show you the statistics of the Monopoly board. Look for: 

• Which sections have higher-than-average landing probabilities? 
• Chance card destinations 
• The properties between Jail and the GoTo Jail space. 
• Railroads. 
• Keep in mind that the Go To Jail space (30) transports you directly to the Jail space (10).

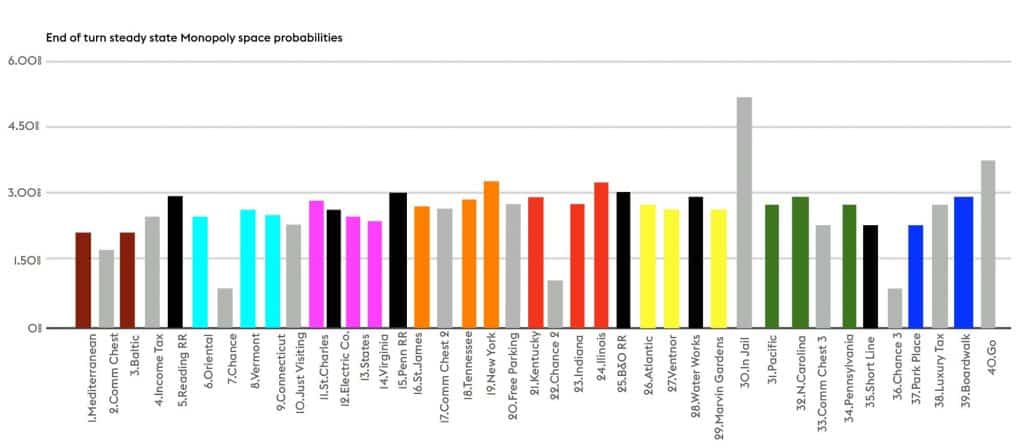
So what can we learn? The red and orange properties are excellent investments. Significantly earlier in the game, you’ve got to get the railroads. Properties between Jail and Go To Jail get landed on more frequently than properties between Go To Jail and Jail.

Other stats we learn from this analysis. On any given turn, a player lands on an average of 1.25 spaces. This is the result of either rolling doubles or hitting a Chance or Community Chest space. The average net income a player receives from one round of play on the board is $170. This includes rents, payments, and the Go space. A factor that stat into your willingness to stay in jail. 

Using Statistics to Get the Best Return on Investments When Building Houses

So when should you build? This is one of the most unshakable questions of Monopoly theory. The next two paragraphs will show you charts from Tim Darling, who has done exceptional research into the best return on investment strategies for construction.

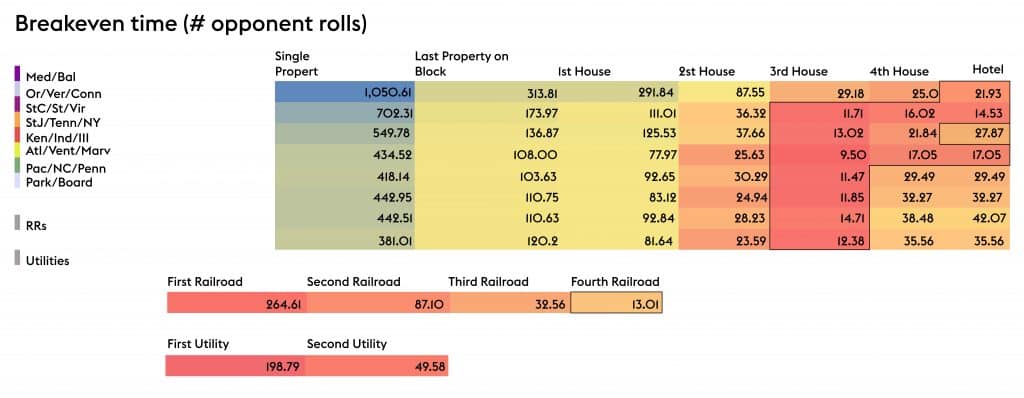
Breakeven time for acquisition & construction

A major question for players is the question of how long it will take them to recoup their investment. This chart shows the average number of opponent rolls before the cost of buying and building houses is recouped. Red means faster-recouped costs, blue means slower.

The total cost of acquisition and construction

Here’s a similar chart showing the total cost of acquisition and construction for each set of properties. The section with the best ROI times is still highlighted with a black border.

So here’s what we know from this: While Park Place and Boardwalk are excellent for crushing opponents early in the game, their ROI is non-ideal. Owning all the railroads is a prime position to be in. Monopoly’s best investment is building the third house on the orange block of St James, Tennessee, and New York. Three houses are the way to go.

So What did we learn?

Lesson #1: Take a chance on these properties 

• NewYork Ave and the orange block 
• Illinois Ave and the red block 
• St. Charles Place and the purple block 
• Boardwalk and the blue block
• The railroads 

Buy the properties and blocks that the Chance card sends you to. These have a higher-than-average rate of being landed on. 

Lesson #2: Everybody needs a place to crash after a night in jail. Jail is the axis of the board. It’s the space that everyone is most likely to end their turn on. Buy up the properties that come to a little bit, after all, precisely the orange, red, and yellow blocks. 

Lesson #3: These are the most commonly landed spaces. Buy them: 

1. Jail  
2. Illinois Ave 
3. New York Ave 
4. Go
5.  B&O Railroad
6. Pennsylvania Railroad
7. Reading Railroad
8. Tennessee Ave 
9. Kentucky Ave
10. Free Parking 
11. WaterWorks 
12. St. James 
13. Atlantic Ave 
14. Indiana Ave 
15. North Carolina Ave 
16. St. Charles Place 
17. Second Community Chest 
18. Ventnor Ave
19. Pennsylvania Ave
20. Boardwalk 

Lesson #4: Your opponent will probably move seven spaces. This is a tactical point. Your opponents are likely to roll a seven and very likely to roll a number very close to seven. When planning your construction, keep this in mind to crush your enemies with crippling rents.