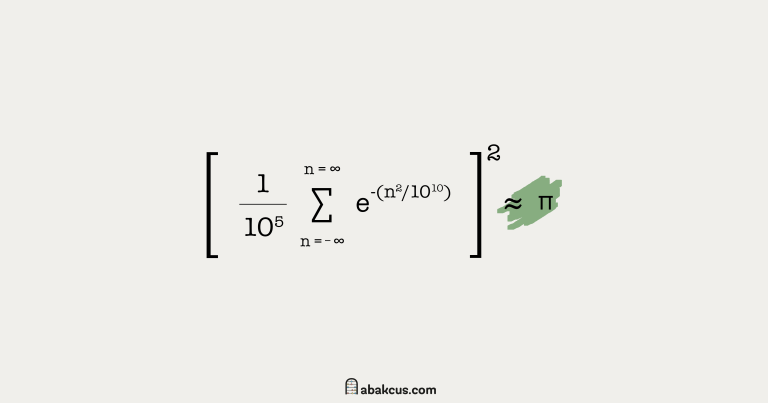
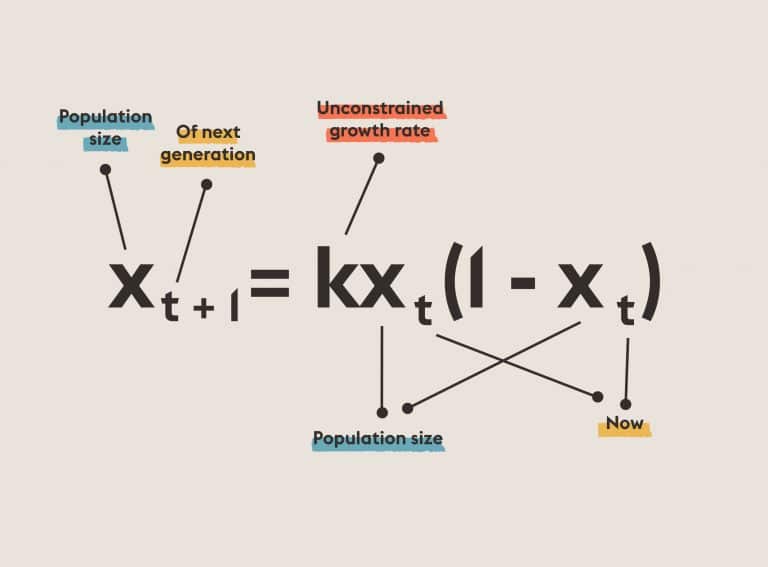
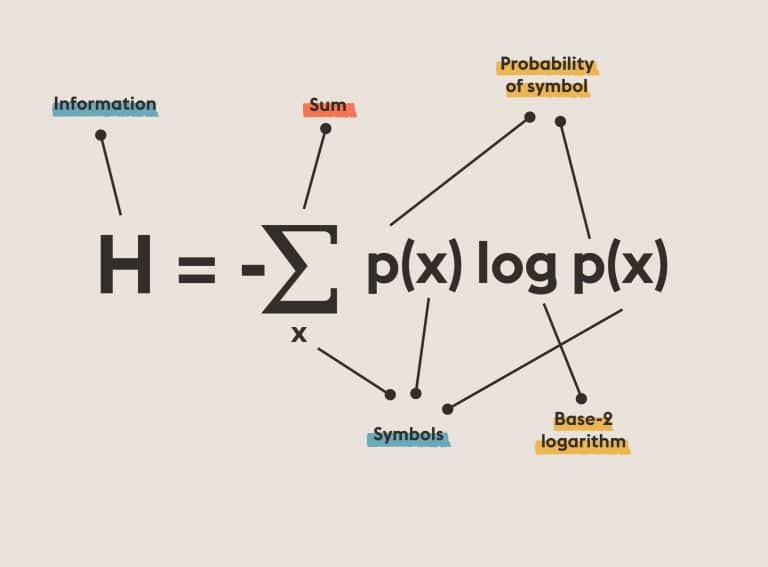
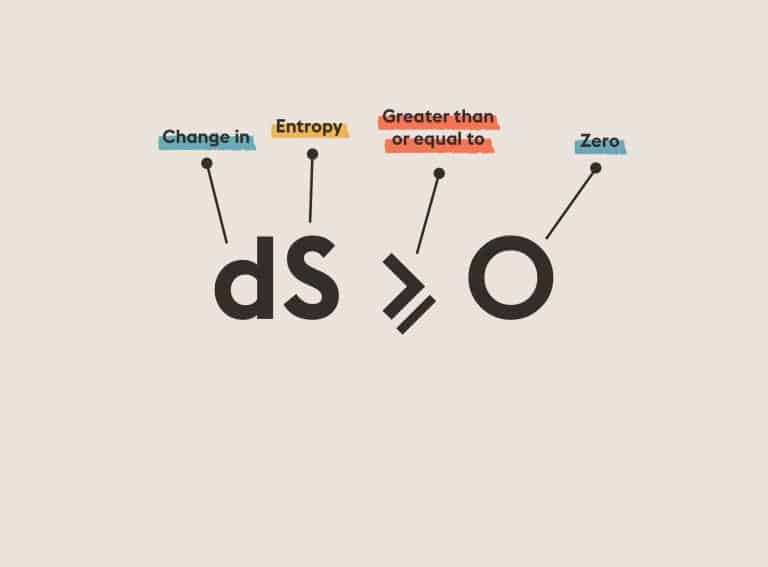
Arbitrary Quadratic Forms: Solving quadratic forms with algebraic numerical coefficients
Hilbert’s 11th problem also concerns algebraic number fields. A quadratic form is an expression, like x2 + 2xy + y2, with integer coefficients in which each term has unknowns raised to a total degree of 2. The number 9 can be represented using integers in the above quadratic form — set x equal to 1 and y equal to 2 — but the number 8 cannot be represented by integers in that quadratic form. Some different quadratic forms can represent the same sets of whole numbers. Hilbert asked for a way to classify quadratic forms to determine whether two forms represent the same set of numbers. Some progress has been made, but the question is unresolved.