If you’ve ever sat in a trigonometry class and felt your brain melt while trying to memorize the unit circle, you’re not alone. Every math student has been there — staring at that mysterious circle filled with angles, coordinates, and Greek letters, wondering why on earth someone thought this was a good idea. But here’s the secret: the unit circle isn’t meant to be memorized through brute force. Once you understand how it’s built, you’ll realize it follows a beautiful, logical pattern that’s surprisingly easy to remember.
Let’s take a calm, visual, and step-by-step journey into how to memorize the unit circle once and for all — without flashcards, panic, or sleepless nights.
The Beauty Behind the Unit Circle
At its core, the unit circle is simply a circle with a radius of one, centered at the origin of a coordinate plane. Every point on this circle represents an angle, and its coordinates correspond to the cosine and sine of that angle. That means if you know the coordinates, you know everything — the sine, the cosine, and even the tangent (which is just sine divided by cosine).
The trouble is that the unit circle introduces so many new things at once: degrees, radians, square roots, and symmetry. Most students try to memorize all the values by heart — which is like trying to learn a song by memorizing every note individually instead of recognizing the melody.
But here’s the trick: you don’t need to memorize it all. You just need to understand the pattern behind it.
Step 1: Draw the Framework
Start by drawing a small table — two columns and five rows. Label the left column “sine” and the right column “cosine.” Then write the main angles down the side: 0°, 30°, 45°, 60°, and 90°. These five are all you need to unlock the rest of the circle.
You can also write their radian equivalents next to them if you like:
0° = 0, 30° = π/6, 45° = π/4, 60° = π/3, 90° = π/2.
This is the skeleton of the first quadrant — the foundation of the unit circle.
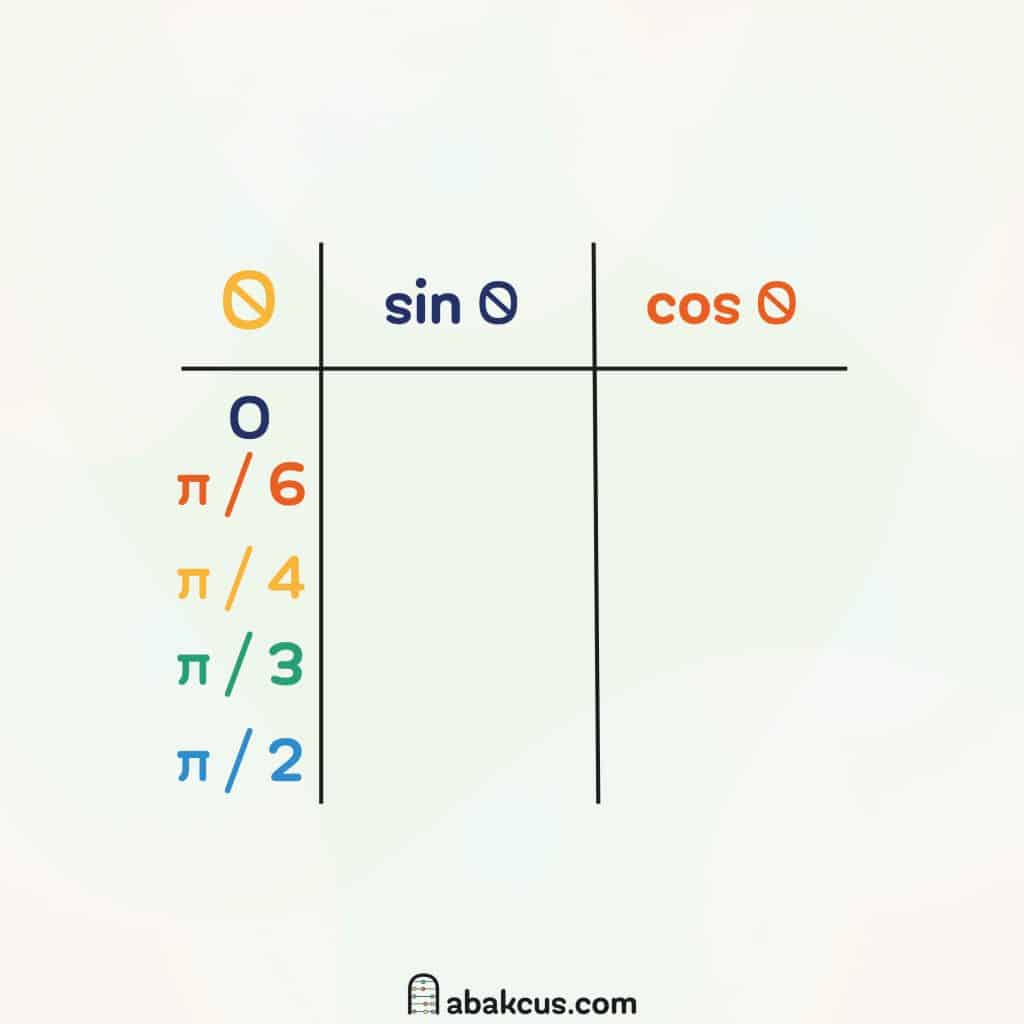
Step 2: Add the Denominators
Now, in each box of your sine and cosine columns, write a denominator of 2. Every sine and cosine value in the first quadrant has a denominator of 2. It’s one of those patterns that’s so simple you’d never notice it if you were just copying the circle from a textbook.
So your table should now look like this (without the numerators yet):

Step 3: Add the Square Roots
Here comes the fun part. In the sine column, you’ll count up from 0 to 4. In the cosine column, you’ll count down from 4 to 0. Each number gets a square root symbol on top.
That gives you:

Step 4: Mirror the Pattern
Now that you know the first quadrant, the rest of the circle practically builds itself. The other three quadrants are reflections and sign changes of this one.
For example:
- In Quadrant II, sine is positive, cosine is negative.
- In Quadrant III, both are negative.
- In Quadrant IV, sine is negative, cosine is positive.
You can fill in every single coordinate (x = cos θ, y = sin θ) just by changing signs accordingly. That’s the magic of symmetry.


Step 5: Connect Angles and Coordinates
Each point on the unit circle corresponds to (cos θ, sin θ). So:
- 0° → (1, 0)
- 30° → (√3/2, ½)
- 45° → (√2/2, √2/2)
- 60° → (½, √3/2)
- 90° → (0, 1)
Notice something? The coordinates are just swapped and mirrored versions of each other. Once you get the rhythm, you can move around the entire circle without hesitation.

Why This Method Works
This approach works because your brain loves structure. Random numbers are hard to recall, but patterns are sticky. When you understand that every sine and cosine in the first quadrant is just a permutation of the numbers 0, 1, 2, 3, and 4 — all divided by 2 and wrapped in square roots — suddenly everything clicks.
You’re not trying to memorize the unit circle anymore. You’re rebuilding it every time you need it. That’s much easier and much more satisfying.
And because it’s visual, it taps into multiple memory systems — spatial, visual, and numerical. The next time you’re solving a trigonometric equation, your brain will automatically recall the pattern, not a list of disconnected values.
Pro Tips for Remembering Faster
- Draw It Repeatedly.
Every time you sketch the unit circle, you strengthen your memory. Even five minutes of practice will make it feel natural. - Say It Out Loud.
As you write, speak: “Sine goes up from zero, cosine goes down from two.” It sounds silly, but it cements the rhythm. - Use Color.
Highlight positive vs negative regions. Mark sine values in blue, cosine in red. Your visual memory will do the rest. - Connect to the Real World.
Think of the unit circle like a compass — every point is a direction. The more you relate it to spatial intuition, the less abstract it feels. - Practice With Radians.
Once degrees make sense, rewrite the same circle in radians (π/6, π/4, π/3, etc.). The structure stays identical.
The “Aha” Moment
At some point, something magical happens: you stop trying to memorize and start to see. You see the circle, the symmetry, the beauty of the numbers dancing around the origin. You realize that trigonometry isn’t about memorization — it’s about relationships and geometry.
When you can memorize the unit circle this way, math stops feeling like a list of rules and starts feeling like a language you understand.
Beyond Memorization
Once you master the unit circle, doors open. Suddenly, concepts like reference angles, trigonometric identities, and even complex numbers begin to make sense. The unit circle becomes your anchor point — the Rosetta Stone of trigonometry.
Every sine wave, every graph, every tangent function you’ll ever see comes from this one idea: a point moving around a circle of radius one.
That’s why it’s worth learning it deeply — not just for your next exam, but because it helps you see how geometry and algebra come together in a single, elegant picture.
In Short
To memorize the unit circle easily, remember:
- Every sine and cosine value comes from the same simple table.
- Sine counts up; cosine counts down.
- Denominators are always 2.
- The pattern repeats in every quadrant with different signs.
That’s all. You’ve cracked one of the most feared topics in trigonometry with logic instead of repetition.
And once you see that pattern, you’ll never forget it again.







