On November 26, 1949, Albert Einstein published an essay in the Saturday Review of Literature in which he described two pivotal moments in his childhood. The first involved a compass that his father showed him when he was four or five. Einstein recalled his sense of wonderment that the needle always pointed north, even though nothing appeared to be pulling it in that direction. He came to a conclusion, then and there, about the structure of the physical world: “Something deeply hidden had to be behind things.” The second moment occurred soon after he turned twelve, when he was given “a little book dealing with Euclidean plane geometry.” The book’s “lucidity,” he wrote—the idea that a mathematical assertion could “be proved with such certainty that any doubt appeared to be out of the question”—provoked “wonder of a totally different nature.” Pure thought could be just as powerful as geomagnetism.
This month, we celebrate the hundredth anniversary of Einstein’s general theory of relativity, one of his many ideas that brought lucidity to the deeply hidden. With all the surrounding hoopla, it would be nice if we could fathom something of what he actually accomplished and how he did it. That turns out to be a tall order, because general relativity is tremendously complex. When Arthur Eddington—the British astrophysicist who led the team that confirmed Einstein’s predictions, during a solar eclipse in 1919—was asked if it was really true that only three people in the world understood the theory, he said nothing. “Don’t be so modest, Eddington!” his questioner said. “On the contrary,” Eddington replied. “I’m just wondering who the third might be.”
Fortunately, we can study an earlier, simpler example of Einstein’s thinking. Even before he received the little geometry book, he had been introduced to the subject by his uncle Jakob, an engineer. Einstein became particularly enamored of the Pythagorean theorem and—“after much effort,” he noted in the Saturday Review—he wrote his own mathematical proof of it. It is my intention to lead you through that proof, step by logical step. It’s Einstein’s first masterpiece, and certainly his most accessible one. This little gem of reasoning foreshadows the man he became, scientifically, stylistically, and temperamentally. His instinct for symmetry, his economy of means, his iconoclasm, his tenacity, his penchant for thinking in pictures—they’re all here, just as they are in his theory of relativity.
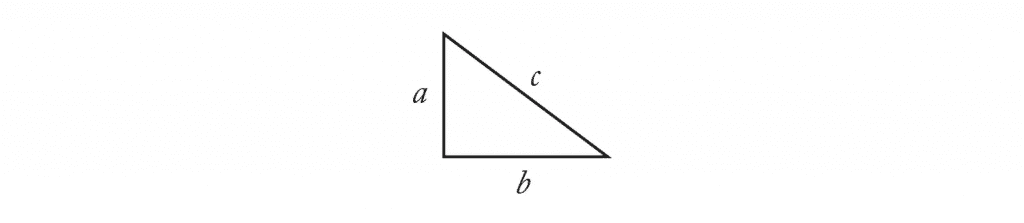
You may once have memorized the Pythagorean theorem as a series of symbols: a2 + b2 = c2. It concerns right triangles, meaning triangles that have a right (ninety-degree) angle at one of their corners. The theorem says that if a and b are the lengths of the triangle’s legs (the sides that meet at the right angle), then the length of the hypotenuse (the side opposite the right angle) is given by c, according to the formula above.
For a clue to that last question, consider the etymology of the word geometry. It derives from the Greek roots g____ē (meaning “earth” or “land”) and metria (“measurement”). It’s easy to imagine ancient peoples and their monarchs being concerned with the measurement of fields or plots of land. Officials needed to assess how much tax was to be paid, how much water they would need for irrigation, how much wheat, barley, and papyrus the farmers could produce.














